Click through the steps below to compare your explanation to a possible response.
In this section, you will use deductive logic to prove some of these conjectures are true beyond a doubt. Let's look at one example.
Conjecture: If a quadrilateral is a square, then it has congruent diagonals. Is this statement true for all cases?
In your notes, explain why the conjecture above must always be true.
Click through the steps below to compare your explanation to a possible response.
Interactive popup. Assistance may be required.
In the example above, you used deductive reasoning to show that any square has congruent diagonals. You can also use deductive reasoning to make formal arguments to prove conjectures about rectangles.
Complete the following deductive argument and prove the conjecture is true by dragging each of the tiles to the proper blank in the deductive argument. Use the Reset button if necessary to reset the interactive.
Deductive reasoning is a process of using statements and ideas that you know to be true in order to prove new statements and ideas. How did you use deductive reasoning to show that the diagonals of a rectangle are always congruent?
Interactive popup. Assistance may be required.
You used previously known statements and ideas (theorems and postulates), including the definition of a parallelogram, definition of vertical angles, congruence of alternate interior angles, triangle congruence theorems, and corresponding parts of congruent triangles (CPCTC) to construct an argument showing that a new statement or conjecture must be true.
Use the theorem and postulate box below to complete the proof of the conjecture. You may use some theorems or postulates more than once.
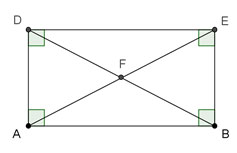
Given rectangle ABED, show that DF ≅ EF .
