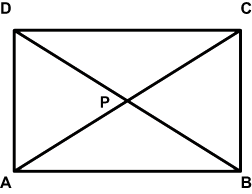
Given: In Rectangle ABCD, the intersection of the diagonals is point P.

A rectangle is a parallelogram, so opposite sides are parallel and

, making

Vertical angles are congruent, so

.

.

Alternate interior angles formed by a transversal intersecting parallel lines are congruent, so

.

ΔAPD ≅ ΔCBP, because of

.

Therefore, DP ≅ BP and

by

.

The diagonals bisect each other by definition of segment bisector.

This deductive argument proves the conjecture correct. Diagonals of a rectangle bisect each other.