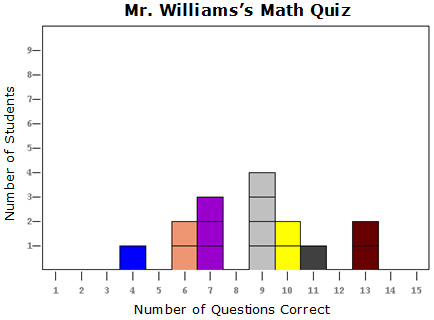
Several types of graphs show the distribution of a data set.

A line plot shows the distribution of a data set by placing a marker on a number line for each data value. The more frequently a data value occurs, the higher the stack of markers.

A stem-and-leaf plot places the hundreds and/or tens digit in one column and the ones digit in another column in order to show the spread of a set of data. The stem and leaf plot shown represents the heights, in meters, of the 15 tallest buildings in the United States.

In this part of the resource, you will investigate histograms, which are commonly used to show the distribution of a set of data.

A histogram appears like a bar graph in that data are represented using bars. However, there are some important differences.

Click the image below to open a histogram generator in a new window.

• Use the data set titled, “Colleges’ SAT Math Scores.”
• Observe the initial graph, including the frequency of data values along the vertical axis.
• One at a time, change the interval size to each of the following values, and observe the effect on the histogram each time.

Use your observations to answer the questions beneath the image.

Need additional instructions?

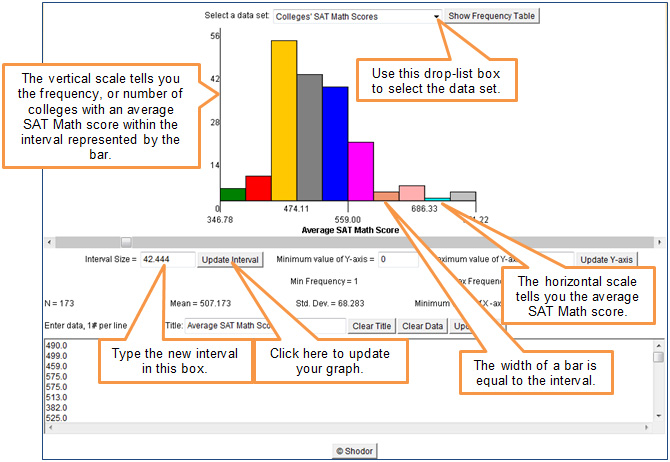
How does the width of each bar change as the interval becomes smaller?

Check Your Answer

Each bar becomes narrower as the interval becomes smaller.

How does the shape of the graph change as the interval becomes smaller?

Hint

If you connected the top of each bar with a smooth curve, what would that curve look like?

Check Your Answer

The cluster of tall bars seems to widen and include more bars as the interval becomes smaller.

How does the width of each bar change as the interval becomes larger?

Check You Answer

Each bar becomes wider as the interval becomes larger.

How does the shape of the graph change as the interval becomes larger?

Hint

If you connected the top of each bar with a smooth curve, what would that curve look like?

Check Your Answer

The tall bars seem to move toward the left, and the bars on the right of the graph get shorter.

In the context of the data presented in this graph (colleges’ average math SAT scores), what does the shape of the histogram tell you?

Hint

Each bar represents the number of colleges with an average math SAT score in that interval.

Check Your Answer

Taller bars represent more colleges with an average math SAT score in that interval. Most of the taller bars are to the left of the middle of the graph (about 556), implying that most colleges have a lower than “middle” average math SAT score.

How might an interval be used to create a misleading histogram?

Possible Answer

An interval that is too small or too large may create misleading conclusions about the distribution of the data set, leading the reader to believe that higher frequencies of data occur where they may not really be occurring.

How is a histogram different from a bar graph?

Possible Answer

A bar graph is used for categorical data, which show the frequency of the number of data points within a category; the horizontal axis will have text labels. A histogram uses intervals to show the frequency of the number of data points within a numerical interval; the horizontal axis will have numerical labels.

How is a histogram different from a line plot? How are they related?

Possible Answer

A histogram uses bars that are the same width as an interval to display the distribution of a data set. A line plot uses individual markers to tally the number of times a particular data value occurs in a data set. They both show the distribution of data within a set, including the frequency of repeated values, but a line plot shows each individual value where a histogram focuses on data values within an interval.

Practice

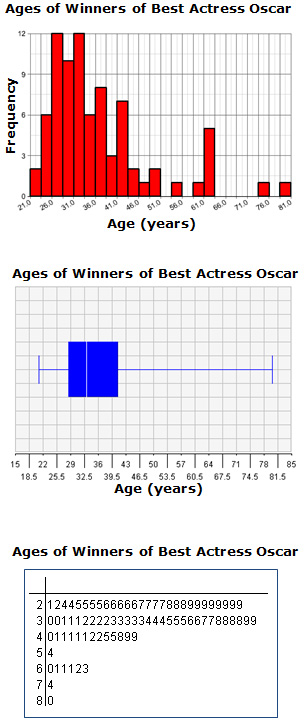
Each of the graphs shown represents the ages of the winners of the Oscar for Best Actress, when they received the award, from 1929 until 2012. For each statement given, identify the graph which best supports the statement.

1. Half of the winners of the Best Actress Oscar were between the ages of 28 and 41 when they received the award.

Interactive popup. Assistance may be required.

Check Your Answer

The box-and-whiskers plot best reveals
this information.
2. More actresses in their 30s won the Best Actress Oscar than actresses in their 20s.

Interactive popup. Assistance may be required.

Check Your Answer

The stem-and-leaf plot best reveals
this information.
3. A significant portion of the Best Actress Oscar winners were at least 26 years old and no more than 32 years old.

Interactive popup. Assistance may be required.

Check Your Answer

The histogram best reveals this
information.
4. The range of winners of the Best Actress Oscar is 59 years.

Interactive popup. Assistance may be required.

Check Your Answer

This statement is supported by
both the box-and-whiskers plot and
the stem-and-leaf plot.
5. 75% of the winners of the Best Actress Oscar are 41 years old or younger.

Interactive popup. Assistance may be required.

Check Your Answer

The box-and-whiskers plot best reveals
this information.