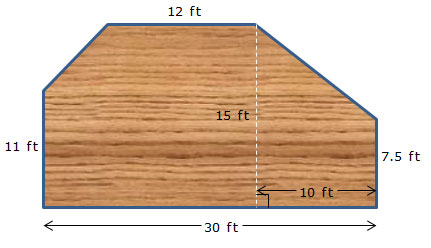
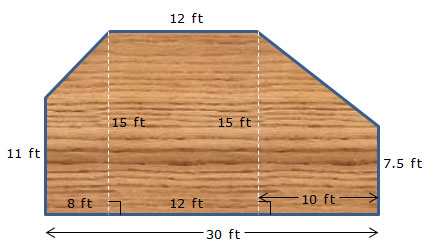
In the last two sections, you practiced breaking a composite figure into component regions. These regions should have simple area formulas. In this section, you will apply that knowledge to solving both mathematical and real-world problems.

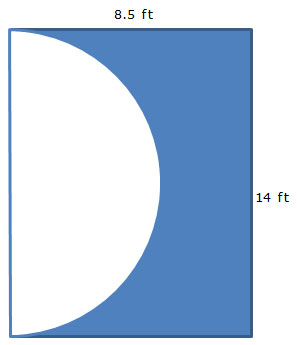
Sometimes, a composite figure contains a hole or a region that must be removed when determining the area of the composite figure.

What operation describes removing, or taking away, a quantity?

Interactive popup. Assistance may be required.

Check Your Answer

Subtraction describes removing, or taking away, a quantity.

Use the interactive below to practice solving problems involving composite figures that are made up of polygons or parts of circles. On screen directions will be provided. You will be asked to identify the component polygons and/or circles. Identify the necessary area formulas, and calculate the area of each component polygon and/or circle. Work through several problems before returning to the lesson. When you click the image below, the interactive will appear in a new browser tab or window.

Interactive popup. Assistance may be required.

Need additional directions?

Sometimes, you have to remove a region from a composite figure when you are determining its area.

Watch the video below to see how to use subtraction when determining the area of a composite figure.

Pause and Reflect

How can you tell whether you need to add or subtract areas of component regions of composite figures?

Interactive popup. Assistance may be required.

Check Your Answer

If you are combining the area of two non-overlapping component regions, then you will add the regions. If you need to remove the area of an overlapping component region, then you will subtract the regions.

Practice

1. A graphic designer created a new logo for a company that will be printed on a large sign. The logo is a rectangle that has a semicircular piece removed. What is the approximate area of the shaded part of the logo?
   
   
   Interactive popup. Assistance may be required.

   Need a hint?

   The formula for the area of a rectangle is A = bh, and the formula for the area of a circle is A = πr². How does the diameter of the semicircle relate to the dimensions of the rectangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   Area of Rectangle = bh = (8.5)(14) = 119 ft²
   Area of Semicircle = 1 over 2 1 2 πr² ≈ 1 over 2 1 2 (3.14)(7)² ≈ 76.93 ft²
   Area of Shaded Region = Area of Rectangle − Area of Semicircle
   Area of Shaded Region ≈ 119 ft² − 76.93 ft² ≈ 42.07 ft²
2. Determine the area of the floor of a room shown in the figure below.
   
   
   Interactive popup. Assistance may be required.

   Need a hint?

   How can you break the figure into rectangles, trapezoids, or triangles?
   Interactive popup. Assistance may be required.

   Check Your Answer

   
   
   Area of Left Trapezoid = 1 over 2 1 2 (11 + 15)(8) = 104 ft²
   Area of Middle Rectangle = 12(15) = 180 ft²
   Area of Right Trapezoid = 1 over 2 1 2 (7.5 + 15)(10) = 112.5 ft²
   Area of Floor = Area of Left Trapezoid + Area of Rectangle + Area of Right Trapezoid
   Area of Floor = 104 ft² + 180 ft² + 112.5 ft² = 396.5 ft²