The volume of a prism is the number of cubic units required to fill the solid figure. Volume is measured in cubic units. They are called cubic units because they are little cubes that are one unit long, one unit wide, and one unit high. They could be any unit of measure; inches, centimeters, feet, yards, etc.
Unit of Length |
Unit of Volume |
Inches |
Cubic Inches |
Centimeters |
Cubic centimeters |
Feet |
Cubic feet |
To find the volume of a rectangular prism, count the number of cubic units in one layer, count the number of layers needed to completely fill the figure, and then multiply them together.
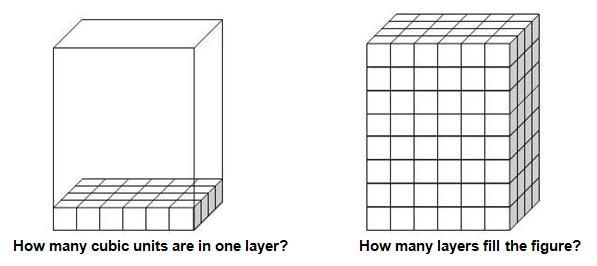
Example: Find the volume of the rectangular prism.

Answer the following questions using the figures in the illustration above. Click on the blank space to check your answers.
Interactive popup. Assistance may be required.
24
Interactive popup. Assistance may be required.
8
Interactive popup. Assistance may be required.
24 x 8 = 192
 of the rectangle.
of the rectangle. of the prism.
of the prism.
Interactive popup. Assistance may be required.
V = l x w x h = Bh
An upper case B is used to represent the area of the base of the prism.
The formula for the volume of the prism is:
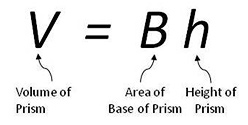
**Lower case b and h are the length and height of an individual polygon. Upper case B refers to the area of a polygonal base of the prism.
Prisms are named according to the shape of their base. A prism's base can be any polygon. The upper case B refers to the area of any shape of the base.