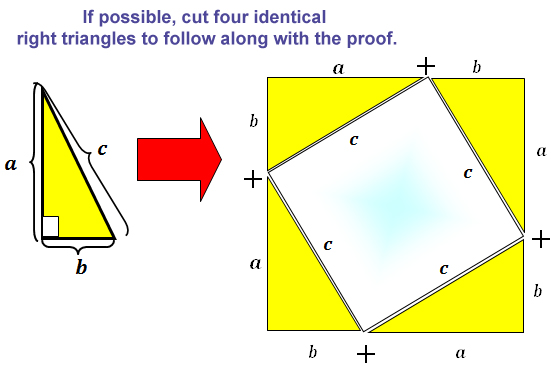
A theorem is a conjecture that has been proven to be true. There are more than 200 documented proofs of the Pythagorean Theorem.

The following is a “proof” for the Pythagorean Theorem based on geometry and algebra.

1. What is the side length of the larger square? Interactive popup. Assistance may be required. Check Your Answer a + b
2. What is the area of the larger square? Interactive popup. Assistance may be required. Check Your Answer The area of the large blue square is: s2 = (a + b)2 = a2 + 2ab + b2
3. What is the area of one triangle? Interactive popup. Assistance may be required. Check Your Answer The area of one triangle is: A = 1 2 bh = 1 2 ab
4. What is the total area of all 4 triangles combined? Interactive popup. Assistance may be required. Check Your Answer The area of all 4 triangles combined is:

5. If you take away the area of the four triangles from the larger square, you will be left the area of which figure?

Check Your Answer The white square in the middle of the figure.

6. What are the dimensions and area of this figure?

Interactive popup. Assistance may be required.

Check Your Answer

The side length of this square is c. Its area is:

A = s² = c²

7. Subtract the algebraic expression representing the total area of the four triangles from the algebraic expression representing the area of the larger square.

Interactive popup. Assistance may be required. Check Your Answer

a² + 2ab + b² - 2ab = a² + b²

Journal Entry: Compare your answers to the last two questions. What do you notice?

Interactive popup. Assistance may be required. Possible Response

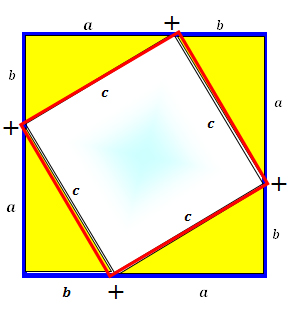
The red square is left once the areas of the triangles are subtracted from the blue square. One side of the red square measures: c The area of the red interior square is: A = c2 OR c2 = a2 + b2 This is the same as the Pythagorean Theorem!