In this section, you will write a verbal description of the given quadratic equation.

A verbal description of a quadratic functions graph mentions
✔Possible roots include: real, rational, irrational or imaginary numbers.
✔ Remember you must actually know the numerical value to be able to decide whether that number is rational or irrational.
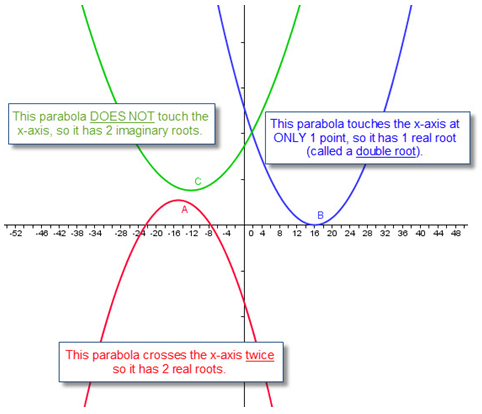
✔ Study the graphs below to determine from a graph whether a parabola has real or imaginary roots.
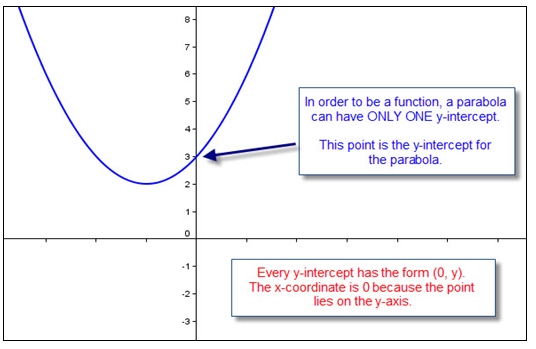
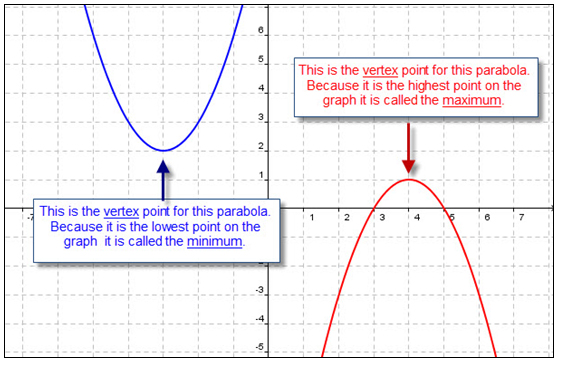
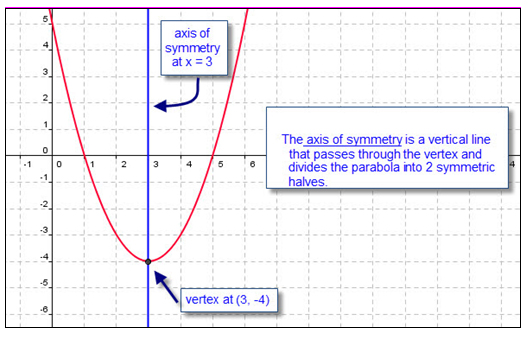
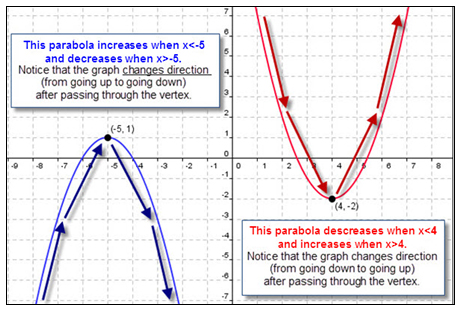
When you need to write a verbal description for a quadratic function using its graph, you can identify its critical attributes and behavior which include:

Write a verbal description for y = 2(x – 3)2 – 8

The terms zeros, roots, and x-intercepts all refer to the same thing.
Simplify first then use any of these methods to solve for x:
y = 2(x – 3)2 – 8
0 = 2(x – 3)2 – 8
0 = 2x2 – 12x + 10
Solving for x → x = 1 or x = 5, both of which are rational real numbers.
The function has 2 real rational roots and the x-intercepts are at (1, 0) and (5, 0).
y = 2(x – 3)2 – 8
y = 2(0 – 3)2 – 8
y = 2(- 3)2 – 8
y = 2(9) – 8
y = 10
The function has a y-intercept at (0, 10).

Remember that anytime you square a number it becomes positive, like (3)2 = 9 or (- 4)2 = 16.
However, if a negative sign is in FRONT of parentheses it is NOT included when squaring and then the answer is negative.
Example: - (5)2 = - 25, because it really means – (5 * 5) which is - 25.

y = a(x – h)2 + k
y = 2(x – 3)2 – 8
h = 3 and k = - 8
The vertex of the parabola is at (3, - 8)
While standing on a 10 foot ladder, Annie threw a beach ball into the air. The height in feet of the beach ball can be modeled by the equation f(t) = - 2t2 + 8t + 10 where t represents the time in seconds after Annie lets go of the ball and f(t) represents its height above the ground in feet.
To find the height, substitute the time into the function.
* (1 minute 30 seconds = 1.5 minutes, so use t = 1.5)
f (t) = - 2t2 + 8t + 10
f (1.5) = - 2(1.5)2 + 8(1.5) +10
f (1.5) = - 2(2.25) + 12 +10
f (1.5) = 17.5
After 1 minute 30 seconds, the beach ball was 17.5 feet above the ground.
When the ball touches the ground, its height is 0 → f(t) = 0
Solve:
f(t) = -2t2 + 8t + 10
0 = - 2t2 + 8t + 10
0 = - 2 (t2 - 4t – 5)
0 = - 2 (t + 1) (t – 5)
t = - 1 or 5
Since t represents time and time cannot be negative, then t = - 1 is an extraneous solution.
Therefore, t = 5 is the ONLY possible solution.
The beach ball reached the ground 5 seconds after she released it.
Remember: Maximum values are found at the vertex of the parabola.
For an equation written in standard form, use the formula x = − b over two a b 2a to find the vertex.
f(t) = - 2t2 + 8t + 10 → a = - 2 and b = 8
x = −
b over two a
b
2a
= −
eight over two times negative two
(8)
2(-2)
= −
eight over negative four
(8)
-4
= −(-2) = 2 → the x–coordinate of the vertex is 2.
To find the y-coordinate, substitute x = 2 seconds into the equation.
f(t) = - 2t2 + 8t + 10
f (2) = - 2(2)2 + 8(2) + 10
f (2) = - 8 + 16 + 10
f (2) = 18 feet
Two seconds after she threw the ball it reached a maximum height of 18 feet.