Source: Conic Section Explorer, Illuminations
In the video, you saw how the four conic sections are formed. Now, let’s study the definitions of those figures.
The conic section that you have already studied is the parabola. Those studies centered on the instances when the parabola represented a quadratic function. Not all parabolas are functions. Turn that parabola on its side and you have a figure that is a quadratic relation, not a function. (Remember, all functions are relations but not all relations are functions.)
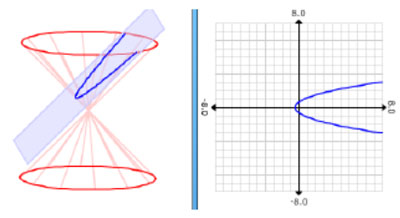
A parabola is defined as the conic section formed when a plane parallel (having the same slope) to the generator line intersects one nappe of a cone.
In the figure below, you can see that the plane is parallel to the cone’s generator line. The graph shows the intersection of the cone and plane. Remember, as stated in the video, the cone only consists of the “skin” and not the interior. The parabola pictured is not a function.

Source: Conic Section Explorer, Illuminations
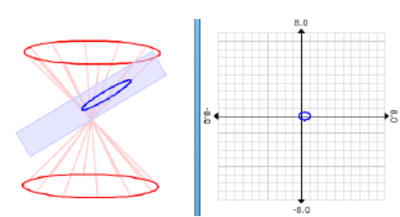
An Ellipse is defined as the conic section formed when a plane that slants with a slope less than the slope of the generator line intersects one nappe of a cone.
An example of an ellipse is pictured below. Because the ellipse is near the vertex, it is not very large.
Source: Conic Section Explorer, Illuminations
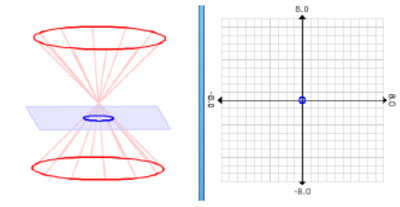
A Circle is defined as the conic section formed when a plane that is perpendicular to the axis of symmetry intersects one nappe of a cone. Because the slope of the plane is less than the slope of the generator line, a circle is a special type of ellipse.
A circle is pictured below with the plane perpendicular to the axis of symmetry of the cone. Again, because the plane is so close to the vertex, the circle is very small.
Source: Conic Section Explorer, Illuminations
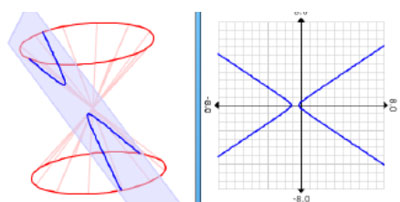
The final major conic, the Hyperbola is defined as the conic section formed when a plane that slants with a slope greater than the slope of the generator line intersects both nappes of a cone
An example of a hyperbola is shown below. You can see that the slope of the plane is steeper than the slope of the generator line. Because the plane is so close to the vertex of the cone, the vertices of the hyperbola are close together.
Source: Conic Section Explorer, Illuminations