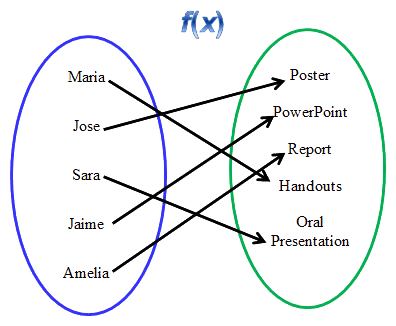
A mapping diagram is similar to a table and a flow chart. When you are working in a group preparing a project for school, each student in your group is often assigned a duty to accomplish in order to complete the project. A mapping diagram can be used to visually represent each student’s task.
The first mapping shows how a group divided up the tasks for a project.
The teacher would probably ask each group which student was doing a given task. If she did, then that would be the inverse of the mapping diagram.
Move the person to the correct task to create the inverse of the mapping function.
Mapping diagrams are related to tables. To examine this relationship, let’s first review the function, f(x) shown in the mapping diagram below.
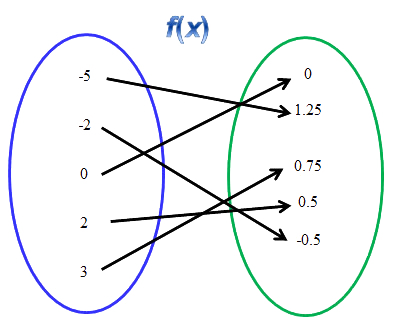
Move the values from the blue oval to the x column in the table below and then move the values in the green oval to the y column.
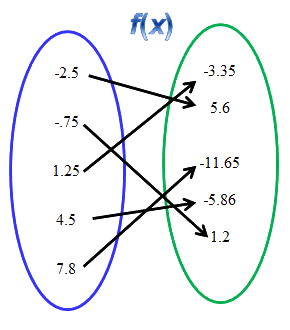
Create the inverse of the function for the mapping diagram by moving the values and the arrows to the correct location.
Interactive popup. Assistance may be required.
-2
Interactive popup. Assistance may be required.
Both a mapping diagram and a table have x- and y-values, and they are both in the same general location. In a mapping diagram, the x’s are in the first oval, and the y’s are in the second oval. In a table, x’s are in the first column and the y’s are in the second column. The difference is that a mapping diagram uses arrows to point out the corresponding y-values whereas in a table the corresponding y-values are directly across from the x-values.
Finding the inverse of a function for a mapping diagram is similar to finding the inverse of a function represented by a table. They both follow the definition for the inverse of a function. Describe the inverse of a function.
Interactive popup. Assistance may be required.
For a function that is defined to be the set of all ordered pairs (x, y), the inverse of the function is the set of all ordered pairs (y, x). The domain of the function becomes the range of the inverse of the function. The range of the function becomes the domain of the inverse of the function.
For a function where every x-value has only one y-value, would the inverse of the function be a function, as well? Explain why or why not.
Interactive popup. Assistance may be required.
Yes. If there is a one-to-one correspondence between the y- and x-values, then the inverse will be a function. In order to test if there is a one-to-one correspondence, use the horizontal line test for a graph, check to see if there is only one y-value for each x-value in a table, or check to see if there is more than one arrow pointing to a value in the second half of the mapping diagram.
Interactive popup. Assistance may be required.
Construct a table or two ovals with the values in them to view the mapping.
Interactive popup. Assistance may be required.
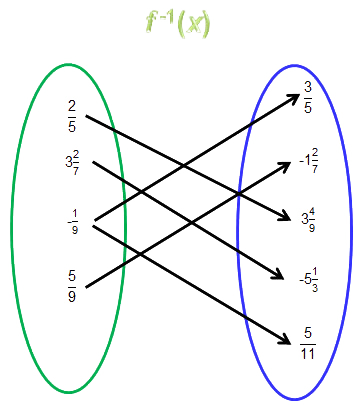
8 map to -5 in f -1(x)
Interactive popup. Assistance may be required.
Draw a mapping for the inverse function.
Interactive popup. Assistance may be required.
Yes, the inverse of the function is a function, because each independent value in the inverse relation maps to only one value.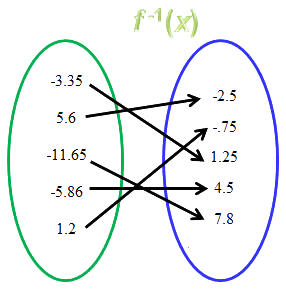
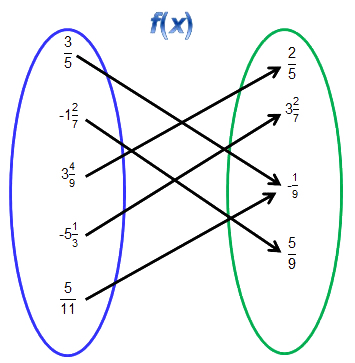
Interactive popup. Assistance may be required.
Draw a mapping for the inverse function.
Interactive popup. Assistance may be required.
No, the inverse is not a function since 1 over 9 - 1 9 maps to both 3 over 5 3 5 and 5 over 11 5 11 .