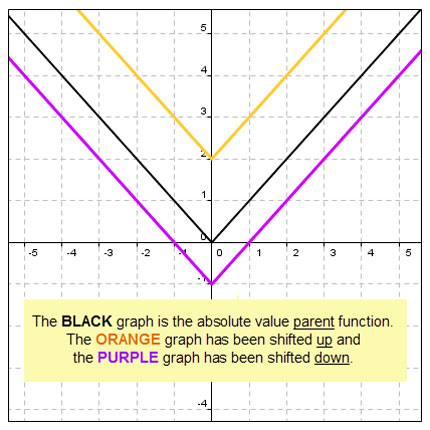
In this section, the change in “k” will be evaluated in the function f(x) = a | x - h | + k.
The absolute value function f(x) = a | x - h | + k translates the absolute value graph up or down.

What happens if we change “k” in y = a | x - h | + k?
![]() To view the affects “k” has on the absolute value function, view this applet and slide the third slider in the lower left hand corner back and forth observing the change in the graph.
To view the affects “k” has on the absolute value function, view this applet and slide the third slider in the lower left hand corner back and forth observing the change in the graph.
Evaluate the function by looking at the tables of values.
y = | x |
x |
y |
4 |
4 |
3 |
3 |
2 |
2 |
1 |
1 |
0 |
0 |
-1 |
1 |
-2 |
2 |
-3 |
3 |
-4 |
4 |
and
y = | x | + 2
x |
y |
4 |
6 |
3 |
5 |
2 |
4 |
1 |
3 |
0 |
2 |
-1 |
3 |
-2 |
4 |
-3 |
5 |
-4 |
6 |
and
y = | x | − 2
x |
y |
4 |
2 |
3 |
1 |
2 |
0 |
1 |
-1 |
0 |
-2 |
-1 |
-1 |
-2 |
0 |
-3 |
1 |
-4 |
2 |
**Notice the repeating y – values in all three tables. The y – value that doesn’t repeat is the vertex. In the second table, the vertex is at (0,2), moving the graph 2 units up; and in the third table, the vertex is at (0,-2), moving the graph 2 units down.
Answer the following questions.
When “k” is positive, the absolute value graph moves ______.
When “k” is negative, the absolute value graph moves ______.