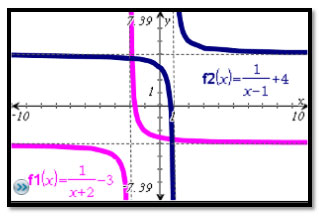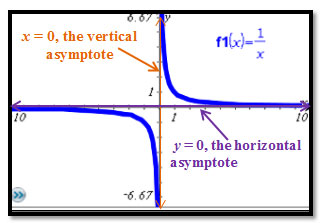
The parent rational function, f(x) = 1 over x 1 x , has a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. Changing the parameters a, h, and k, will change the intersection point of the asymptotes. This point will help you when describing the transformation that has occurred.

What happens to the graph of a rational function when you change the parameters of a, h, and k?

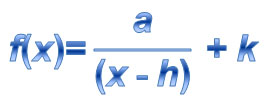
In the interactive below, set b = 1. Begin with only changing the value for a, leaving h and k equal to zero. Then, change only the value of h, leaving a = 1 and k = 0. Finally, change only the value of k, leaving a = 1 and h = 0.

Interactive popup. Assistance may be required.

Need additional directions?

Conclusion Questions

• What happened to the graph when you increased the value of a (a > 1)?

  Interactive popup. Assistance may be required.

  Check Your Answer

  As the value of a increased (a > 1), the graph was vertically stretched.

• What happened to the graph when you decreased the value of a (0 < a < 1)?

  Interactive popup. Assistance may be required.

  Check Your Answer

  As the value of a got closer to 0, the graph was vertically compressed.

• What happened to the graph when the value of a became negative?

  Interactive popup. Assistance may be required.

  Check Your Answer

  When the value of a became negative, the graph reflected across the horizontal asymptote.

• What happened to the graph when you increased or decreased the value of h?

  Interactive popup. Assistance may be required.

  Check Your Answer

  As the value of h increased, the function shifted to the right. As the value of h decreased, the function shifted to the left.

• What happened to the graph when you increased or decreased the value of k?

  Interactive popup. Assistance may be required.

  Check Your Answer

  As the value of k increased, the function shifted up. As the value of k decreased, the function shifted down.

• How did the vertical and horizontal asymptotes change with respect to changing the values of h and k?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The vertical asymptote intersects the x-axis at the value of h, and the horizontal asymptote intersects the y-axis at the value of k.

Pause and Reflect

How were the methods used in this lesson to transform the rational function similar to those used to transform other types of functions, such as quadratics or exponential functions?

Interactive popup. Assistance may be required.

Check Your Answer

The effects in changes of a, h, and k are the same regardless of the function family. Changing the value of a results in a vertical stretch or compression, and changing the sign of a results in a reflection across a horizontal axis. Changing the value of h results in a horizontal shift, and changing the value of k results in a vertical shift.

Now think about the square root function f(x) = a√(x – h) + k. What do you predict will happen when changes are made to a, h, and k?

Interactive popup. Assistance may be required.

Check Your Answer

Changing the value of a will cause a vertical stretch or compression; changing the value of h will cause a horizontal shift; and changing the value of k will cause a vertical shift.

Practice

1. Describe the transformation of the graph of the parent function f(x) = 1 over x 1 x to the graph of the rational function f(x) = 3 over x 3 x .

   Interactive popup. Assistance may be required.

   Need a hint?

   The change is in a, and its value is greater than 1.

   Interactive popup. Assistance may be required.

   Check Your Answer

   The graph of the parent function is vertically stretched by a factor of 3.

2. In f(x) = 3 over x + 5 3 (x + 5) + 8, which value in the function shifted the graph of the parent function vertically?

   Interactive popup. Assistance may be required.

   Need a hint?

   Look for the constant, k, being added or subtracted to the parent function, f(x) = 1 over x 1 x .
   Interactive popup. Assistance may be required.

   Check Your Answer

   8
3. If the graph of f(x) = 1 over x - 3 1 (x – 3) – 9 were shifted horizontally to the right 10 units, what would be the new function?

   Interactive popup. Assistance may be required.

   Need a hint?

   A horizontal shift is a change in h. If the vertical asymptote is originally at x = 3 and you moved it to the right 10 units, the new vertical asymptote would be at x = 3 + 10.
   Interactive popup. Assistance may be required.

   Check Your Answer

   f(x) = 3 over x + 5 1 (x – 13) – 9
4. Describe the transformation from f1(x) that will generate f2(x) in the graph below.
   
   Interactive popup. Assistance may be required.

   Need a hint?

   Locate the point where the horizontal and vertical asymptotes intersect for function f1, and count the units vertically and horizontally to the intersection of the asymptotes for function f2.
   Interactive popup. Assistance may be required.

   Check Your Answer

   Function f2 has been translated up 7 units and to the right 3 units from function f1.