Answer to question 1: No (1 ≠ -1)
Answer to question 2: Yes (-5 = -5)
Answer to question 3: Yes (5 ≥ 5: it is equal)
Answer to question 4: No (-1 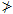 4)
4)

When you are given ordered pairs and asked to determine if it is a solution to a linear equation or inequality, the easiest thing to do is just to substitute the values of the ordered pair into the equation or inequality.
Is (5, -4) a solution to equation 2x + 3y = -2?
If we substitute 5 in for x and -4 in for y, we will have the following:
2x + 3y
2(5) + 3(-4)
10 + (-12)
-2
=
=
=
=
-2
-2
-2
-2
Since we end up with a true statement, we know that (5, -4) IS a solution to the equation.
Is (-1, 2) a solution to the inequality y < 2x + 1?
If we substitute -1 in for x and 2 in for y, we will have the following:
y < 2x + 1
2 < 2(-1) + 1
2 < -2 + 1
2 < -1
Since 2 is NOT less than -1, we know that (-1, 2) is NOT a solution to the inequality.
Now it's time for you to practice. Use your notes and determine if the given ordered pairs are solutions to the linear equations or inequalities.
When you have answered all of the questions, click below.
Interactive popup. Assistance may be required.Answer to question 1: No (1 ≠ -1)
Answer to question 2: Yes (-5 = -5)
Answer to question 3: Yes (5 ≥ 5: it is equal)
Answer to question 4: No (-1 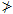 4)
4)
