In the previous section, the first video showed how the equation for direct variation, y = kx, relates to the equation of a line, y = mx + b, with the slope equal to k and a y-intercept of zero; therefore, one point on the line is (0,0).

For this section, you will need to use a graphing utility, such as a graphing calculator or the applet referenced below.

Click on the link to open the applet in a new window in your browser. Use the applet to answer the questions below.

Interactive Slope of a Line

Need help? Interactive popup. Assistance may be required. Click here for additional directions.

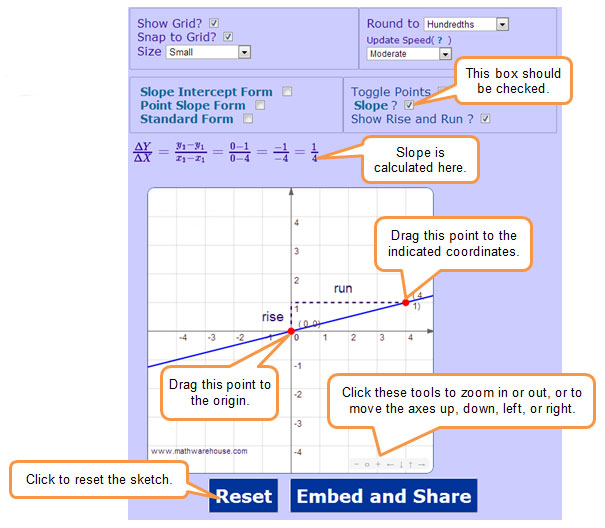
In the applet, move one point to (0, 0), and move the second point to the given coordinates. Find the coordinate(s) that will answer the question.

1. If y varies directly as x and y = 2 when x = 3, find y when x = 9.

   Interactive popup. Assistance may be required.

   Need a hint?

   Move the second point to (3, 2), and zoom out to find the y-coordinate of the point along the line that has the x-coordinate of 9.
   Interactive popup. Assistance may be required.

   Check Your Answer

   y = 6
2. If y varies directly as x and y = 1 when x = 2, find x when y = 5.

   Interactive popup. Assistance may be required.

   Need a hint?

   Move the second point to (2, 1), and zoom out to find the x-coordinate of the point along the line that has the y-coordinate of 5.
   Interactive popup. Assistance may be required.

   Check Your Answer

   x = 10
3. Maria purchased a pencil for $2. The number of pencils varies directly as the cost in dollars. If Maria has $10 to spend, find the number of pencils she can purchase.

   Interactive popup. Assistance may be required.

   Need a hint?

   Let x represent the cost in dollars and y represent the number of pencils. Move the second point to (2, 1), and zoom out to find the y-coordinate of the point along the line that has the x-coordinate of 10.
   Interactive popup. Assistance may be required.

   Check Your Answer

   Maria can purchase 5 pencils.

Pause and Reflect

For a direct variation graph, why does the line always go through the origin?

Interactive popup. Assistance may be required.

Check Your Answer

If the line did not go through the origin, the relationship would not be proportional.

The constant of variation is the value of k in the equation y = kx. How does the constant of variation compare to the slope of the line y = kx?

Interactive popup. Assistance may be required.

Check Your Answer

The constant of variation is equal to the slope of the line.

Practice

Miranda made a graph to show the number of miles she can run for certain times. The number of miles, y, varies directly as the number of hours, x, she runs. Use the graph to answer Questions 1-3.

1. What is the constant of variation shown in the graph?

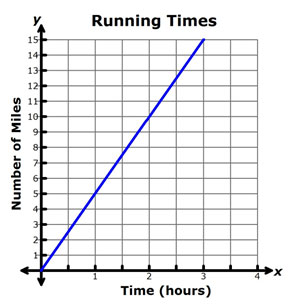
   Interactive popup. Assistance may be required.

   Need a hint?

   What is the slope of the line?
   Interactive popup. Assistance may be required.

   Check Your Answer

   5 miles per hour
2. If Miranda runs 2.5 hours, how many miles will she run?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the y-coordinate of the point along the line with an x-coordinate of 2.5?
   Interactive popup. Assistance may be required.

   Check Your Answer

   12.5 miles
3. If Miranda runs 15 miles, how many hours did she run?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the x-coordinate of the point along the line with a y-coordinate of 15?
   Interactive popup. Assistance may be required.

   Check Your Answer

   3 hours