In the late 1930s, physicists noticed that when a neutron was shot into a 235 92 U nucleus, the nucleus would split into two parts, which would fly apart at tremendous speed and release two or three neutrons. They carefully measured the mass of the resulting pieces and found it to be a little bit less than the mass of the original uranium nucleus.

The following is a nuclear fission simulation.

Click to Run

Source: Nuclear fission, Universtiy of Colorado - Physics

When the simulation opens, use the mouse to click the red button to fire a neutron at a uranium 235 nucleus. After the neutron strikes the nucleus, it will become unstable and finally break apart. Click pause just after the nucleus breaks apart.

Interactive popup. Assistance may be required.

Check Your Answer

The nucleus breaks into 3 neutrons and 2 smaller nuclei.

The actual nuclear equation looks like the following:

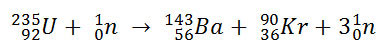
In words, this would read as follows: Uranium-235 is hit by a neutron and breaks into barium-143, krypton-90, and three neutrons. The amount of missing mass from this nuclear reaction was exceedingly small; each uranium atom loses about 0.186 AMU (that's about 3.1 x 10^-28 kg).

This is where one of the most famous equations in physics comes in: E = mc².

Source: Walk Of Ideas, Lienhard Schultz by Scholz& Friends Sensai agency, Wikimedia Commons

The energy released by each uranium fission reaction is equal to the missing mass times the speed of light (3 × 10⁸ m/s) squared. The total amount of energy released by nuclear fission of uranium is 2.787 × 10^-11 J.

So, what's the big deal?

The big deal is that you get that much energy per atom. Just think one gram of uranium-235 has about 2.56 × 10²⁰ atoms, for a total of about 7.14 × 10¹⁰ J!

That is like saying a standard pick-up truck has enough energy to power a city for a year. Take a moment to watch the video below. As you are watching, describe in your notes how the mass-energy equation is shown in nuclear fission.

In the next section, you will look at the relationship between the mass-energy equivalence and nuclear fusion.