Now that you’ve explored the concepts of work and kinetic energy, let’s see how they work together in the work-energy theorem. Watch the following video for an introduction to the work-energy theorem and a review of kinetic energy.
Now that you’ve explored the concepts of work and kinetic energy, let’s see how they work together in the work-energy theorem. Watch the following video for an introduction to the work-energy theorem and a review of kinetic energy.
Source: Work Energy Theorem, Ken Schenck, YouTube
Work and kinetic energy are both scalar quantities measured in joules. They are the same kind of number measured with the same units but are two different ways of describing the same thing.
The work-kinetic energy theorem states that the net work on an object is equal to the change in that object's kinetic energy. That means if you add up the total work done by all the forces on an object, you will know the object's change in KE.
Let's take a closer look at both sides of this equation. On the left side we have Wnet. Wnet, which means the total work done on a system. Either add up the work done by each force, or find the total force and calculate the work done by it. The right column is ΔKE. The Greek symbol Δ means change, so ΔKE = KEf – KEi.
Wnet |
= |
ΔKE |
| Wnet means the total work done on a system. Either add up the work done by each force, or find the total force and calculate the work done by it. | The Greek symbol Δ means change. ΔKE = KEf – KEi KEf — means the final KE KEi — means the initial KE |
Watch the following animation comparing the stopping distances of three cars moving at different velocities.
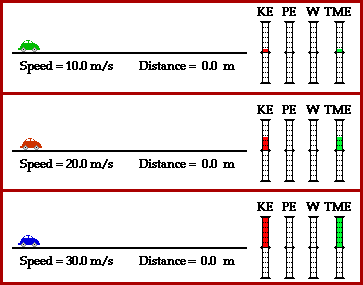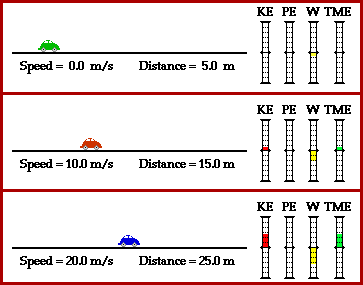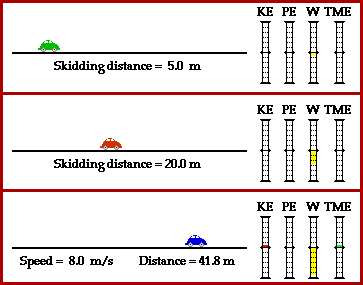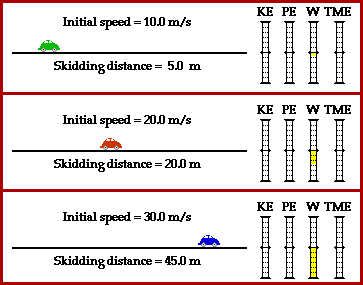
Source: Energy, The Physics Classroom
The four values shown to the right of each car are Kinetic Energy (red), Potential Energy (always zero), Work (yellow), and Total Mechanical Energy (green).
What is friction doing to the velocity of the car in terms of work and energy?
Remember, work-energy theorem predicts the stopping distance by
Fdcosθ = 1 2 mv22 – 1 2 mv12
You can substitute q = 180 since friction is directly opposite displacement and cos(180) = -1, making the left side of the equation
-Fd
You can also plug in v = 0 because the cars are stopping. That makes the right side of the equation
- 1 2 mv12
The negative signs cancel to yield:
Fd =
1
2
mv12
or
d =
mv12
2F
Now that you understand the equation for work (W = Fd) and the equation for kinetic energy (KE = 1/2 mv2), let’s take a moment to practice putting them together in the work-energy theorem.
A 2.000 kg book is accelerated from 2.000 m/s to 4.00 m/s as it is pulled across a table. What is the amount of work needed to accelerate the book to the nearest tenth of a joule?
Wnet = ΔKE
First, you will need to use the Kinetic Energy equation to figure out the ΔKE.
ΔKE = KEf – KEi
Then, solve for ΔKE using the equation for kinetic energy to find Kef and KEi.
KE = ½ mv2
KEf = ½ (2.00 kg) (4.00 m/s)2=16 J
KEi = ½ (2.00 kg) (2.00 m/s)2= 4 J
Now, solve for ΔKE.
ΔKE = KEf – KEi
ΔKE = 16 – 4 = 12 J
Wnet = ΔKE
Wnet = 12 J