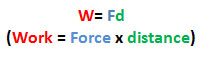
Work equation is
W=Fdcosθ
where
F: force (Newtons)
d: displacement (meters)
θ: the angle between force and displacement (degrees)
This takes into account the angle between the force and the displacement.
For our work now, let’s consider that force and displacement are in the same direction. Since the force and displacement are in the same direction, you don't need to take the angle into account. Therefore, you can use the equation W = Fd.
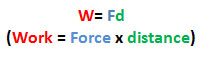
Sometimes you are given information for two of the three parts of the equation and will need to alter the equation to solve it.
In the activity below, match the altered work equation with the correct information.
Calculate work in the practice problems below. The first problem is an example.
A truck hitched to a trailer exerts a horizontal net force of 500.0 Newtons. If the trailer moves a total distance of 1525 meters, how much work was done by the truck?
Work =? force = 500.0 N distance = 1525 meters
Since the force and displacement are in the same direction, you don't need to take the angle into account. The correct formula for this problem is Work = Force distance. Look at the solution below.
= (500.0 N) × (1525m)
= 762,500 Nm
= 762,500 J
= 7.625 X 105 J
Now you try! Set up the problem first. Click on the hint link for a clue.
A student exerts a vertical net force of 175 N on a stack of books. He does 350 J of work on the books. What vertical distance did he move the books? Note: force and displacement are in the same direction; therefore, you will not use the angle θ.
