Recall how Ohm's law can be used within a circuit to calculate current. The same equation is used to calculate the voltage drop across resistors in a circuit. It is called voltage drop because any circuit element that uses energy will show a decrease in electric potential.

Let’s practice calculating voltage by solving the problems below.

Problem 1

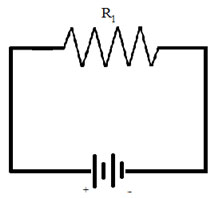
Calculate the potential difference (voltage drop) across the resistor in the following simple circuit if R₁ = 10 Ω and the battery voltage = 3 V.

Interactive popup. Assistance may be required.

Hint 1

The resistor is directly connected to either side of the battery with a wire.

Interactive popup. Assistance may be required.

Solution

Since the resistor is directly connected to either side of the battery with a wire, the voltage drop across the resistor is the same as that of the battery.
V = 3 V

---

Problem 2

Calculate the potential difference (voltage drop) across each of the three resistors in the following circuit if R₁ = 1.0Ω, R₂ = 2.0Ω, and R₃ = 3.0Ω and the battery's voltage = 12 V.

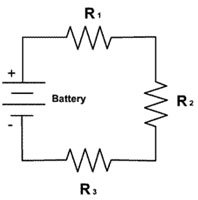Source: DC circuits-series, school for champions

Interactive popup. Assistance may be required.

Hint 1

First, you need to know the voltage in each resistor so you need to know the current running through each one.

Interactive popup. Assistance may be required.

Hint 2

To find the current, calculate the total resistance of the circuit. The correct formula to calculate equivalent resistance for a series circuit is R_T= R₁ + R₂ + R₃.
R_T= 1.0 Ω + 2.0 Ω + 3.0 Ω
R_T = 6.0Ω

Interactive popup. Assistance may be required.

Hint 3

Based on Ohm’s law, use the equivalent resistance to calculate the amount of current leaving the battery.
I = V R
I = 12V 6.0Ω
I = 2.0 A
Since this is a series circuit, the full 2.0 A of current will flow through each of the three resistors.

Interactive popup. Assistance may be required.

Hint 4

In the final step use Ohm's law for each resistor.
V = IR

Interactive popup. Assistance may be required.

Solution

R1 = 1Ω V = IR V = (2.0 A)(1.0Ω) V = 2.0 V

R2 = 2Ω V = IR V = (2.0 A)(2.0Ω) V = 4.0 V

R3 = 3Ω V = IR V = (2.0 A)(3.0Ω) V = 6.0 V

Interactive popup. Assistance may be required.

Check Your Answer

To double-check your work, the sum of all the individual potential differences has to equal the total voltage of the battery.
V₁ = 2.0 V
V₂ = 4.0 V
V₃ = 6.0 V
V_total = V1 + V2 + V3
V_total = 2.0 V + 4.0 V + 6.0 V
V_total = 12 V

---

Problem 3

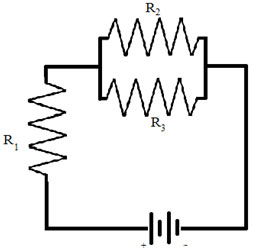
Calculate the potential difference (voltage drop) across each of the three resistors in the following circuit if
R₁ = 1.0Ω, R₂ = 2.0Ω, and R₃ = 3.0Ω and the battery's voltage = 12 V.

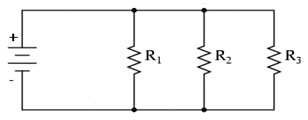Source: DC circuits Parallel, School for Champions

Interactive popup. Assistance may be required.

Hint 1

Identify the type of circuit arrangement: series or parallel.
Since the current flowing from the battery reaches junctions where it can split into separate pathways, this is a parallel circuit.

Interactive popup. Assistance may be required.

Hint 2

Each resistor is connected directly by a wire to each side of the battery.

Interactive popup. Assistance may be required.

Hint 3

The voltage drop across each resistor has to be the same as the voltage drop of the battery.

Interactive popup. Assistance may be required.

Solution

The potential difference (voltage) for R₁, R₂, and R₃ each equal 12 V.

---

Problem 4

Calculate the potential difference (voltage drop) across each of the three resistors in the following circuit if
R₁ = 1.0Ω, R₂ = 6.0Ω, and R₃ = 3.0Ω and the battery's voltage = 9 V.

Interactive popup. Assistance may be required.

Hint 1

You need to find the current running through the entire circuit. The first step is to find R_T.

Interactive popup. Assistance may be required.

Hint 2

Find the resistance of the parallel combination R_P first.
1 R_p = 1 R₂ + 1 R₃
1 R_p = 1 6 + 1 3 (common denominator is 6)
1 R_p = 1 6 + 2 6 = 3 6 = 1 2
R_p = 2Ω

Interactive popup. Assistance may be required.

Hint 3

Now find the total for the whole circuit.
R_T = R₁ + R_P
R_T = 1 + 2 = 3 Ω

Interactive popup. Assistance may be required.

Hint 4

The current through the whole circuit can be found using Ohm's law.
I = V/R
I = 9/3
I = 3 A

Interactive popup. Assistance may be required.

Solution

For the first resistor use the following:
V = IR_I. V + (3 A)(1Ω) = 3 V
Just like in problem 3, the parallel resistors will have the same voltage. The total for the battery is 9 V, and the first resistor uses up 3 V. Therefore, the resistance across R₂ and R₃ has to be 6 V.

---