Adding resistors in parallel is a little bit different than it is in series because every time you add another resistor in parallel, you are adding another path that the charge can take. This is like increasing the area of the wire in the simulation from section 1. It actually reduces the overall resistance of the combination.

Think of it like this. The slowest part of going to the grocery store is usually the checkout line. It acts like a resistor because it makes you move slower. If there is only one line open, it could take a really long time to get out of the store, but if they open more lines, you can get out easier. You are adding more of what slows people down, but it makes it easier for people to get out by giving more possible paths for leaving the store.

The equation for adding resistors in parallel is: 1 RT = ∑ 1 Ri

At first glance you probably want to just take the reciprocal of both sides, and then you have the same equation as you had for series resistors. Unfortunately, the ∑ in the equation won't let you do that. You need to take the reciprocal of each resistance, add them up, and then take the reciprocal of that answer to get the total.

Let's take a look at an example.

Sample Problem

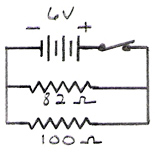
A 6 V battery is connected to an 82Ω resistor and a 100Ω resistor arranged in parallel. Determine the equivalent resistance of the resistor combination.

Identify known variables: R1 = 82 Ω, R2 = 100 Ω

Equation 1 RT = 1 82 + 1 100
Least common denominator is 4100 1 RT = 50 4100 + 41 4100
1 RT = 91 4100
Take the reciprocal of both sides RT = 4100 ÷ 91
Correct answer: RT = 45.5 Ω

Most calculators have a reciprocal key that will look like this: x-1 or this: 1/x

This is how the calculation would look using this key

  1. Equation: RT = (R1-1 + R2-1)-1
  2. Substitute variables: RT = (82-1 + 100-1)-1
  3. Correct answer: 45.05Ω

Now you try this one:

Practice Problem

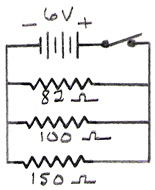
A 6 V battery is connected to an 82Ω resistor, a 100Ω resistor, and a 150Ω resistor. The three resistors are connected in parallel. Determine the equivalent resistance of the resistor combination.

Interactive popup. Assistance may be required.

Need a hint?

Equation 1 RT = ∑ 1 Ri
Substitute values to get 1 RT = 1 82 + 1 100 + 1 150
Least common denominator is 12300 1 RT = 150 12300 + 123 12300 + 82 12300
1 RT = 355 12300

RT = 12300 ÷ 355
Close Pop Up
Interactive popup. Assistance may be required.

Check Your Answer

34.65ΩClose Pop Up
Interactive popup. Assistance may be required.

Reciprocal key solution

1. Equation: RT = (R1 + R2-1 + R3-1)-1

2. Substitute variables: RT = 82-1 + 100-1

3. Correct answer: 34.65ΩClose Pop Up