There are two ways that resistors can be connected in circuits. They can be connected one right after another in a line—series—or they can be connected so that they form two separate branches or paths within the circuit—parallel.
Each time a resistor is added in series to a circuit, it increases the total resistance of a circuit. You just made it that much more difficult for charge to flow. The total resistance (RT) of the circuit is determined by adding up the individual resistances (Ri) of the individual resistors.
The equation for the total resistance is: RT = ∑Ri
∑Ri is a quick math way of writing, "add up all the individual R values you have." It translates to R1 + R2 + R3 + … for as many resistors as you have.
An 82 Ω resistor and a 100 Ω resistor are arranged in series. Determine the equivalent resistance of the resistor combination.
Identify known variables: R1 = 82 Ω R2 = 100 Ω
| Equation: | RT=∑Ri RT=Ri + R2 |
| Substitute values and solve: | RT=82Ω + 100Ω = 182Ω |
| Correct answer: | RT = 182Ω |
| Now you try one: |
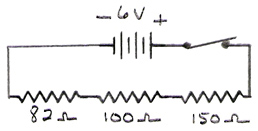
A 6V battery is connected to an 82Ω resistor, a 100Ω resistor, and a 150Ω resistor. The three resistors are connected in series. Determine the equivalent resistance of the resistor combination.
| Identify known variables: | R1=82ΩR2=100ΩR3=150Ω |
| Equation: | RT=∑Ri RT=R1+R2+R3 |
| Substitute values and solve: | RT82ΩR2 + 100Ω + 150Ω = 332Ω |
