In the past, you investigated coordinate translations, reflections, and dilations. Translations are transformations that slide, or translate, a figure over a coordinate plane. Reflections are transformations that create mirror images of figures. Dilations are transformations that generate enlargements or reductions of figures.

In this section, you will extend what you know about coordinate transformations rotations in multiples of 90° and look for patterns in the coordinates.

Part 1: 90° Rotations

Click the image below to open an interactive sketch in a new browser tab or window. Once you have opened the sketch, use the slider to change the angle of rotation to 90° counter-clockwise. Locate the coordinates of the image of the rotation, and complete the table below. Use your table to answer the questions that follow.

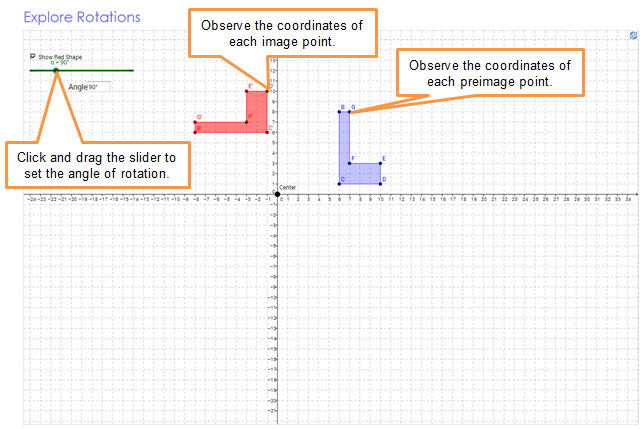
Click to seeInteractive popup. Assistance may be required. additional directions in using the interactive sketch.

Use the interactive sketch to complete the following table for a 90° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.

Interactive popup. Assistance may be required.

Check your Answer

Image Point	Original Coordinates	Rotated Coordinates
B	(6, 8)	(-8, 6)
C	(6, 1)	(-1, 6)
D	(10, 1)	(-1, 10)
E	(10, 3)	(-3, 10)
F	(7, 3)	(-3, 7)
G	(7, 8)	(-8, 7)

Use your completed table to answer the questions that follow.

• What patterns do you observe in the coordinates?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The x-coordinate of the rotated coordinates has the opposite sign of the y-coordinate of the original coordinates.
  The y-coordinate of the rotated coordinates is the same as the x-coordinate of the original coordinates.

• How could you express that relationship using an algebraic rule?

  Interactive popup. Assistance may be required.

  Check Your Answer

  If a polygon is rotated 90° counterclockwise around the origin, the coordinates of each point in the polygon are changed by the following rule:
  (x, y) → (−y, x)

Part 2: 180° Rotations

Use the interactive sketch to complete the following table for a 180° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.

Interactive popup. Assistance may be required.

Check Your Answer

Image Point	Original Coordinates	Rotated Coordinates
B	(6, 8)	(-6, -8)
C	(6, 1)	(-6, -1)
D	(10, 1)	(-10, -1)
E	(10, 3)	(-10, -3)
F	(7, 3)	(-7, -3)
G	(7, 8)	(-7, -8)

Use your completed table to answer the questions that follow.

• What patterns do you observe in the coordinates?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The x-coordinate of the rotated coordinates has the opposite sign of the x-coordinate of the original coordinates.
  The y-coordinate of the rotated coordinates has the opposite sign of the y-coordinate of the original coordinates.

• How could you express that relationship using an algebraic rule?

  Interactive popup. Assistance may be required.

  Check Your Answer

  If a polygon is rotated 180° counterclockwise around the origin, the coordinates of each point in the polygon are changed by the following rule:
  (x, y) → (−x, −y)

Part 3: 270° Rotations

Use the interactive sketch to complete the following table for a 270° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.

Interactive popup. Assistance may be required.

Check Your Answer

Image Point	Original Coordinates	Rotated Coordinates
B	(6, 8)	(8, -6)
C	(6, 1)	(1, -6)
D	(10, 1)	(1, -10)
E	(10, 3)	(3, -10)
F	(7, 3)	(3, -7)
G	(7, 8)	(8, -7)

Use your completed table to answer the questions that follow.

• What patterns do you observe in the coordinates?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The x-coordinate of the rotated coordinates is the same as the y-coordinate of the original coordinates.
  The y-coordinate of the rotated coordinates has the opposite sign of the x-coordinate of the original coordinates.

• How could you express that relationship using an algebraic rule?

  Interactive popup. Assistance may be required.

  Check Your Answer

  If a polygon is rotated 270° counterclockwise around the origin, the coordinates of each point in the polygon are changed by the following rule:
  (x, y) → (y, −x)

Part 4: 360° Rotations

Use the interactive sketch to change the angle of rotation to 360° counter-clockwise. Use the results to answer the questions that follow.

• What happens to the image of the rotation when the preimage is rotated 360°? Why do you think that is the case?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The image and preimage overlap, because a 360° rotation is a full turn.

• How could you express that relationship using an algebraic rule?

  Interactive popup. Assistance may be required.

  Check Your Answer

  If a polygon is rotated 360° counterclockwise around the origin, the coordinates of each point in the polygon are changed by the following rule: (x, y) → (x, y)

Pause and Reflect

How are a 90° counterclockwise rotation about the origin and a 270° clockwise rotation alike? How are they different?

Interactive popup. Assistance may be required.

Check Your Answer

Both rotations generate the same image. The difference is that one rotation turns one direction, and the other rotation turns the opposite direction.

Practice

1. The figure below shows quadrilateral WXYZ.

   

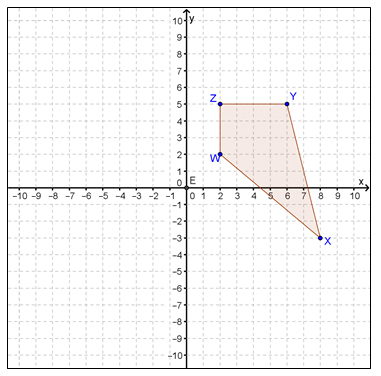
   If WXYZ is rotated 90° counterclockwise about the origin, what will be the coordinates of the image of WXYZ?

   Interactive popup. Assistance may be required.

   Need a hint?

   What algebraic rule describes the results of a 90° rotation that is counterclockwise about the origin?
   Interactive popup. Assistance may be required.

   Check Your Answer

   W' (−2, 2), X' (3, 8), Y' (−5, 6), Z' (−5, 2)
2. In the figure below, pentagon PQRST has been rotated counterclockwise about the origin to generate pentagon P'Q'R'S'T'.

   

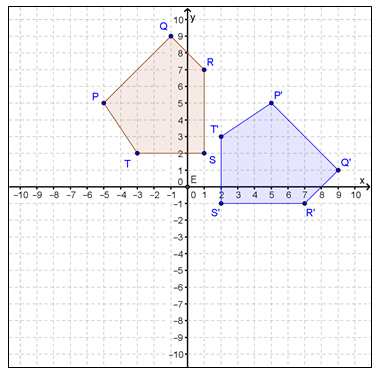
   What is the algebraic rule that best describes the rotation?

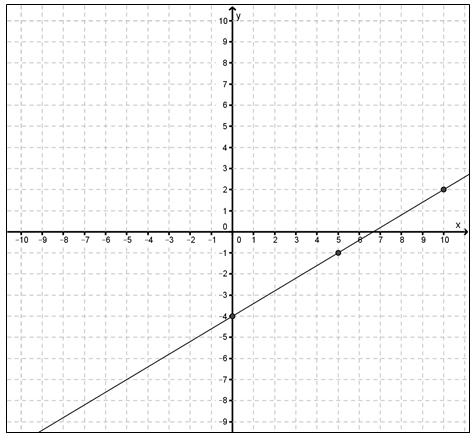
   Interactive popup. Assistance may be required.

   Need a hint?

   How do the coordinates of point T change in order to generate point T'? Check this pattern with another pair of points from the preimage and the image.
   Interactive popup. Assistance may be required.

   Check Your Answer

   (x, y) → (y, −x)

 

3. Which of the following pairs of transformations would generate the same image from the same preimage?
   1. Rotation of 270° counterclockwise about the origin and rotation of 90° clockwise about the origin
   2. Rotation of 180° about the origin and reflection across the line y = -x
   3. Rotation of 90° clockwise about the origin and translation of 4 units right and 5 units down

   Interactive popup. Assistance may be required.

   Need a hint?

   Sketch the results of each transformation for a figure of your choice, and compare the two images (use a reflection interactive, rotation interactive, or translation interactive if necessary). Which of the three pairs gives you the same image?

   
   Interactive popup. Assistance may be required.

   Check Your Answer

   I only