Now that you have investigated with one type of 3-dimensional figure (prisms), let's see if the relationship between the scale factor of a dilated cylinder and the volume holds true as well.
![]() Use the interactive sketch below to dilate Cylinder H using the ScaleFactor slider. Notice how the dilated volume changes as you manipulate the figures in the interactive. Use this interactive sketch to complete the table beneath the sketch.
Use the interactive sketch below to dilate Cylinder H using the ScaleFactor slider. Notice how the dilated volume changes as you manipulate the figures in the interactive. Use this interactive sketch to complete the table beneath the sketch.
Volume of Original Cylinder (H) |
Scale Factor |
Volume of Dilated Cylinder (M) |
(Scale Factor)3 |
Volume of Original Cylinder× (Scale Factor)3 |
24.5 |
2 |
195.99 |
8 |
196 |
24.5 |
1.75 |
|
|
|
24.5 |
1.5 |
|
|
|
24.5 |
0.75 |
|
|
|
24.5 |
0.5 |
|
|
|
Interactive popup. Assistance may be required.
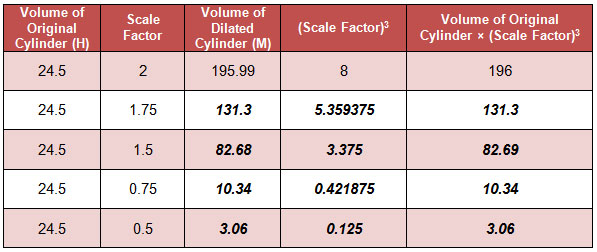

What is the relationship between the volume of the dilated cylinder, the volume of the original cylinder, and the scale factor?
Interactive popup. Assistance may be required. The volume of the dilated cylinder is equal to the product of the volume of the original cylinder and the cube of the scale factor. The area of the dilated circle is equal to the product of the area of the original circle and the square of the scale factor.
The area of the dilated circle is equal to the product of the area of the original circle and the square of the scale factor. 