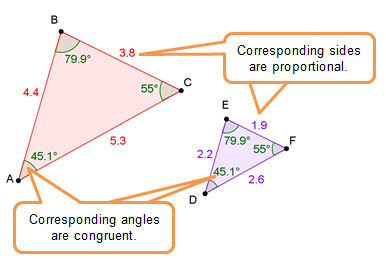
In previous grades, you learned that two figures are similar if all of the corresponding angles are congruent and all of the corresponding side lengths are proportional.

In this section, you will refine what you know about similar triangles in order to make arguments and solve problems about similar triangles when you only know the measures of two pairs of corresponding angles. This condition of similar triangles is called the angle-angle criterion.
![]() Click on the image below to access the interactive. Use the interactive to investigate two triangles, Δ ABC and Δ HGI. Use the sliders to adjust the angle values. Click and drag on points A and B to adjust the size of Δ ABC, and click and drag on points G and I to adjust the size of Δ HGI.
Click on the image below to access the interactive. Use the interactive to investigate two triangles, Δ ABC and Δ HGI. Use the sliders to adjust the angle values. Click and drag on points A and B to adjust the size of Δ ABC, and click and drag on points G and I to adjust the size of Δ HGI.
Use the interactive to answer the questions below.
Interactive popup. Assistance may be required.
Use the triangle sum to find the third angle.
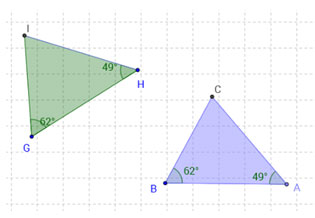
What does this tell you about the measures of the third interior angle in each triangle? Explain your reasoning.
Interactive popup. Assistance may be required.
The corresponding side lengths are proportional.
Interactive popup. Assistance may be required.
The corresponding side lengths are proportional.
Interactive popup. Assistance may be required.
Yes. Since all pairs of corresponding angles have equal measures, they are congruent. Also, all pairs of corresponding sides are proportional.
For the angle-angle criterion for similarity, you know that two pairs of corresponding angles are congruent. Why do we not need to state that the third pair of corresponding angles is also congruent?

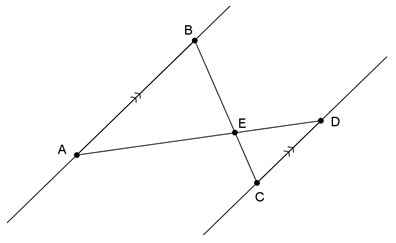


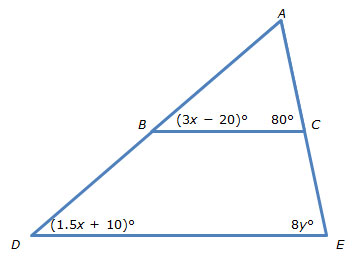
Use the diagram below to answer questions 2 − 4. Assume that BC || DE.
Interactive popup. Assistance may be required.
Identify two pairs of corresponding angles, and apply the angle-angle criterion.
Interactive popup. Assistance may be required.
Solve each equation from question 1 using properties of real numbers and inverse operations.
Interactive popup. Assistance may be required.
Substitute the value of x into the expression for m∠ABC.