In the last section, you investigated relationships between pairs of angles created when a transversal crosses two parallel lines. In this section, you will investigate and use informal arguments to describe two important relationships among the angles of a triangle:
![]() Click on the image below to access the interactive. Use the interactive to investigate the relationship among the measures of the three interior angles of a triangle. Click on the arrow in the bottom left corner or slowly drag the slider at the bottom. Notice the congruent angles.
Click on the image below to access the interactive. Use the interactive to investigate the relationship among the measures of the three interior angles of a triangle. Click on the arrow in the bottom left corner or slowly drag the slider at the bottom. Notice the congruent angles.
Use the interactive to answer the questions below.
Interactive popup. Assistance may be required.
They are alternate interior angles, and they are congruent.
Interactive popup. Assistance may be required.
They are alternate interior angles, and they are congruent.
Interactive popup. Assistance may be required.
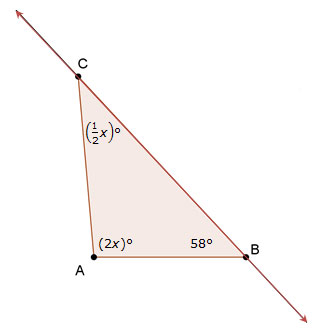
These three angles form a straight line, and a straight line has an angle measure of 180°. The sum of the measures of these three angles must be equal to 180°.
A triangle has several exterior angles, or angles formed outside the triangle by extending one of the three sides. There can be up to six exterior angles depending on which sides are extended.
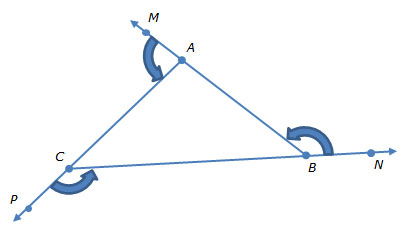
In the diagram shown, triangle ABC has three exterior angles: ∠MAC, ∠ABN, and ∠PCB.
![]() Click on the image below to access the interactive. Use the interactive below to investigate the relationship between an exterior angle of a triangle and the two opposite, or remote, interior angles. Click and drag the red vertex of the triangle to change the shape of the triangle. Use the sliders to move the interior angles to the same vertex as the exterior angle so that you can compare the measures of the three angles.
Click on the image below to access the interactive. Use the interactive below to investigate the relationship between an exterior angle of a triangle and the two opposite, or remote, interior angles. Click and drag the red vertex of the triangle to change the shape of the triangle. Use the sliders to move the interior angles to the same vertex as the exterior angle so that you can compare the measures of the three angles.
Use the interactive to answer the questions below.
Interactive popup. Assistance may be required.
The purple and green interior angles line up along the exterior angle.
Interactive popup. Assistance may be required.
The sum of the measures of the two interior angles is the same as the measure of the exterior angle.
Interactive popup. Assistance may be required.
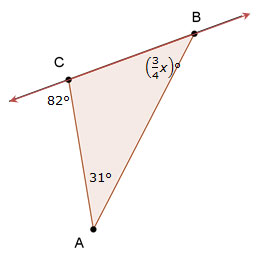
95°, because the measure of the exterior angle is equal to the sum of the measures of the two remote (opposite) interior angles; i.e., 75° + 20° = 95°.
For both the sum of the interior angles of a triangle and the measure of an exterior angle of a triangle, straight lines were important. Thinking about the number of degrees there are in an angle created by one straight line, why do you think that is the case?

 DE ∥ AC. Use the angle relationships created by parallel lines to explain why
DE ∥ AC. Use the angle relationships created by parallel lines to explain why 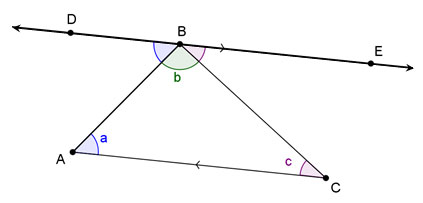
 DE and AC? What is the relationship between ∠EBC and ∠BCA?
DE and AC? What is the relationship between ∠EBC and ∠BCA?