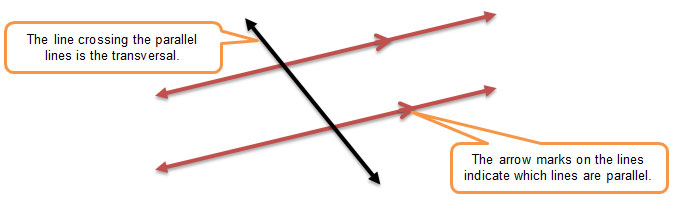
In this section, you will investigate relationships among angle pairs created by two parallel lines that are crossed by a transversal.

![]() Use the interactive below to investigate the five relationships of angles formed by parallel lines and a transversal. Click the image to open the interactive, and it will open in a new browser tab or window. Drag the blue points to change the transversal. As you do so, notice how the angle measured for the eight labeled angles change.
Use the interactive below to investigate the five relationships of angles formed by parallel lines and a transversal. Click the image to open the interactive, and it will open in a new browser tab or window. Drag the blue points to change the transversal. As you do so, notice how the angle measured for the eight labeled angles change.
Use the interactive to answer the questions below.
Interactive popup. Assistance may be required.
Corresponding angles have equal measures.
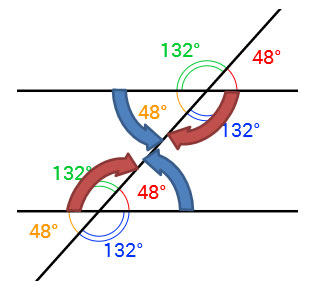
What do you notice about the measures of alternate interior angles?
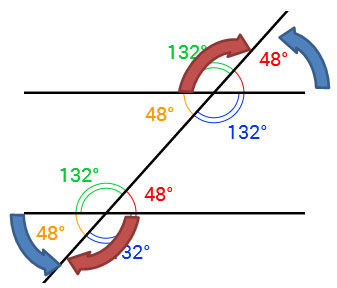
What do you notice about the measures of alternate exterior angles?
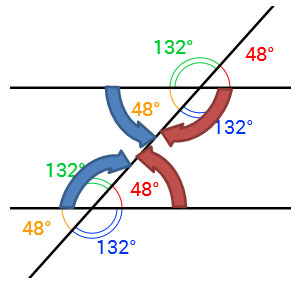
What do you notice about the measures of consecutive interior angles?

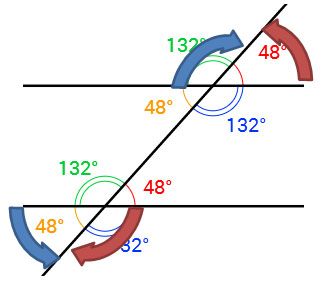
What do you notice about the measures of consecutive exterior angles?
What patterns do you see in angle pairs that are congruent?

What patterns do you see in angle pairs that are supplementary?
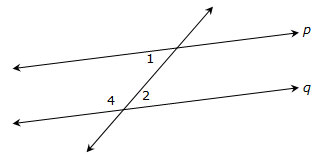
In the diagram below, transversal l crosses parallel lines b and c. Use this diagram to answer questions 2 and 3.
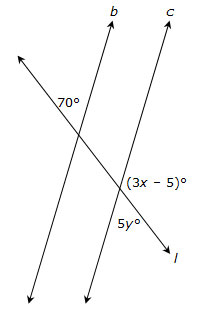
Interactive popup. Assistance may be required.
Identify the angle marked with an expression containing x and an angle with a given measurement. What is the relationship between these two angles?
Interactive popup. Assistance may be required.
Identify the angle marked with an expression containing y and an angle with a given measurement. What is the relationship between these two angles?
Interactive popup. Assistance may be required.
Solve the equations from questions 2 and 3.