Cylinders will also frequently appear in surface area problems.

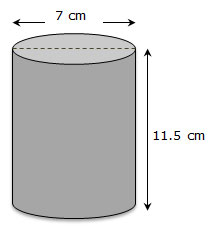
A sardine factory uses steel cans to package sardines. The cans are in the shape of cylinders. One can that they use is shown below.

cylinder with dimensions labeled
Interactive exercise. Assistance may be required.

The factory engineer wants to know the area of the label of the can. Drag the dimensions from the Dimensions Box onto the appropriate place in the formula to calculate the lateral surface area of the can.


Now that you have correctly identified the dimensions, calculate the area of the label of the can, or the lateral surface area of the can.

Interactive popup. Assistance may be required.

Check Your Answer

80.5Π ≈ 252.77 square centimetersClose Pop Up Interactive exercise. Assistance may be required.

The factory engineer also wants to know how much steel is required to manufacture one can. Drag the dimensions from the Dimensions Box onto the appropriate place in the formula to calculate the total surface area of the can.

Now that you have correctly identified the dimensions, calculate the amount of steel required to manufacture one can, or the total surface area of the can.

Interactive popup. Assistance may be required.

Check Your Answer

80.5Π + 24.5Π = 105Π ≈ 329.7 square centimetersClose Pop Up

Video segment. Assistance may be required.This activity might not be viewable on your mobile device. View a video to see a detailed solution.

Practice

  1. A cylindrical poster tube is wrapped completely for shipping. What is the approximate amount of paper required, not counting any waste, to completely cover the cylinder?

    2. cylinder with dimensions labeled
    Interactive popup. Assistance may be required.

    Hint

    The amount of paper required to completely cover the cylinder will be equal to the total surface area of the cylinder, SA = 2πrh + 2πr2. Don't forget to use the radius, even though the diameter is the measurement shown.Close Pop Up Interactive popup. Assistance may be required.

    Check Your Answer

    2π(21 over 4 1 4 )(22) + 2π(21 over 4 1 4 )2 = 99π + 101 over 8 1 8 π = 1091 over 8 1 8 π ≈ 342.65 square inchesClose Pop Up
  2. A cylindrical water tank will be painted such that all exposed faces will be painted with weatherproof blue paint.

cylinder with dimensions labeled

What will be the approximate total area of the water tank that is painted blue? Round your answer to the nearest hundredth.

Interactive exercise. Assistance may be required. Use the grid below to record your answer. Type your answer in the boxes in front of and behind the decimal. Click inside each box to enter the numeral that belongs in the box, and then click the bubble beneath the numeral to shade the bubble that matches the numeral. Incorrect portions of your answer will be shaded gray.

Interactive popup. Assistance may be required.

Hint

The only faces that will be painted are the lateral surface and the roof of the tank. The base of the cylinder resting on the ground will not be painted.Close Pop Up

Click "Show Answer" to confirm that your gridded response is correct.