
In the previous section, you looked for relationships between the volume formulas for prisms and pyramids. In this section, you will investigate relationships between cylinders, cones, and spheres.
Volume of Cylinders

![]() Click on the image below to access the interactive to investigate the formula for the volume of cylinders. Follow the onscreen prompts until you reach the summary screen in the interactive.
Click on the image below to access the interactive to investigate the formula for the volume of cylinders. Follow the onscreen prompts until you reach the summary screen in the interactive.
NeedInteractive popup. Assistance may be required. 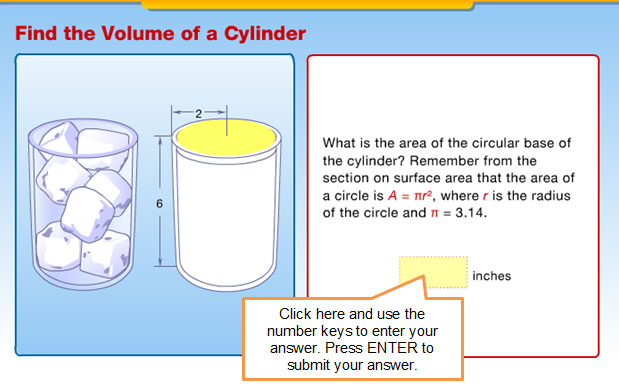
 ?
?
What was the area of the circular base of the cylinder?
What was the height of the height of the cylinder?
How did you determine the area of the base?

What was the volume of the cylinder?
How is the volume of a cylinder related to the area of the base of the cylinder and the height of the cylinder?

![]() In the following interactive, drag the appropriate symbols into the appropriate place to build a formula for calculating the volume of any cylinder. You may use the tiles more than once.
In the following interactive, drag the appropriate symbols into the appropriate place to build a formula for calculating the volume of any cylinder. You may use the tiles more than once.
Volumes of Cones and Spheres
Cones and spheres have a special relationship to cylinders. As with pyramids and prisms, let’s begin by thinking about a cylinder, cone, and sphere with congruent dimensions:
![]() The animation below shows the same cylinder and cone from the diagram. Use the animation to see how many times you need to fill the cone and pour it into the cylinder before you have a completely full cylinder.
The animation below shows the same cylinder and cone from the diagram. Use the animation to see how many times you need to fill the cone and pour it into the cylinder before you have a completely full cylinder.
How many times did you need to fill the cone and pour it into the cylinder in order to completely fill the cylinder?
Interactive popup. Assistance may be required.3 times 
If the formula for the volume of a cylinder is V = Bh, what is the formula for the volume of a cone?
Interactive popup. Assistance may be required.V = 1 over 3 1 3Bh
If the formula for the volume of a cylinder is V = πr2h, what is the formula for the volume of a cone?
Interactive popup. Assistance may be required.V = 1 over 3 1 3πr2h
![]() The animation below shows the same cone and sphere from the diagram. Use the animation to see how many times you need to fill the cone and pour it into the sphere before you have a completely full sphere.
The animation below shows the same cone and sphere from the diagram. Use the animation to see how many times you need to fill the cone and pour it into the sphere before you have a completely full sphere.
How many times did you need to fill the cone and pour it into the sphere in order to completely fill the sphere?
Interactive popup. Assistance may be required.2 times 
If the formula for the volume of a cone V = 1 over 3 1 3πr2h, what is the formula for the volume of a sphere?
Interactive popup. Assistance may be required.V = 2 x1 over 3 1 3πr2h = 2 over 3 2 3πr2h
If the “height” of the sphere is equal to the diameter (2 times the radius, or 2r), how does that change your volume formula for a sphere?
Interactive popup. Assistance may be required.V = 2 over 3 2 3πr2 (2r) = 4 over 3 4 3πr3
![]() Match each figure below with an expression that could be used to determine its volume. Move the expression to see the original formula from which it comes.
Match each figure below with an expression that could be used to determine its volume. Move the expression to see the original formula from which it comes.