Click on the image below to access the interactive to investigate the formula for the volume of prisms. Follow the onscreen prompts until you reach the summary screen in the interactive.Volume of Prisms
To begin this section, let's take a look back at how to determine the volume of prisms.
Click on the image below to access the interactive to investigate the formula for the volume of prisms. Follow the onscreen prompts until you reach the summary screen in the interactive.
NeedInteractive popup. Assistance may be required.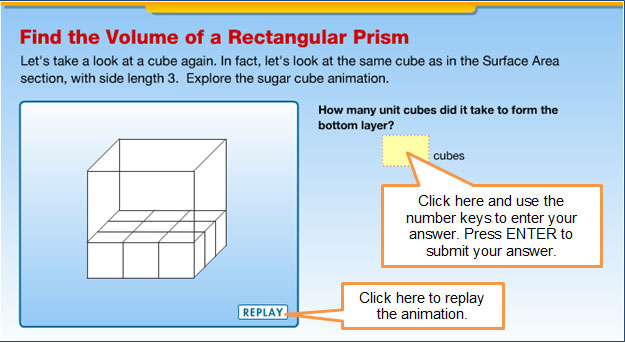 
?
How many unit cubes did it take to form the bottom layer of the cube?
Interactive popup. Assistance may be required.
9 units
How many of these layers would it take to fill the entire cube?
Interactive popup. Assistance may be required.
3 layers
In total, how many of the unit cubes were needed to fill the cube or polyhedron?
Interactive popup. Assistance may be required.
27 units
How did you determine the area of the base layer?
Interactive popup. Assistance may be required.
One way to determine the area is to multiply the base length by the base width.
How did you determine the total number of cubes it took to fill the large cube?
Interactive popup. Assistance may be required.One way to determine the total number of cubes is to multiply the area of the base by the number of layers (height of the prism).
In the following interactive, drag the appropriate symbols into the appropriate place to build a formula for calculating the volume of any prism.
Volume of Pyramids
Now that you’ve written a general formula for the volume of any prism, let’s extend that to write a formula for the volume of a pyramid.
Recall that a prism and a pyramid both have polygonal bases. Let’s consider a prism and a pyramid that have congruent bases and the same height as shown in the image below.
Use the animation below to pour the volume of one pyramid into a prism with a congruent base and the same height.
If the height of the prism is 10 units, about how high will the liquid from the pyramid fill the prism?
Interactive popup. Assistance may be required.
Both the pyramid and the rectangular prism have the same height, 10 units but, the pyramid appears to be smaller than the rectangular solid, in other words, if the pyramid were put inside the prism it would not fill it up. When the liquid is poured from the pyramid into the prism the liquid fills about 3.3 units.
In general, for any height of prism and pyramid, about how high will the liquid from the pyramid fill the prism?
Interactive popup. Assistance may be required.
Since 3.3 units of liquid moved from the pyramid into the prism, the liquid filled about 1 over 3 1 3 the height of the prism.
In the following interactive, drag the appropriate symbols into the appropriate place to build a formula for calculating the volume of any pyramid.
Practice
Match each figure below with an expression that could be used to determine its volume. Move the expression to see the original formula from which it comes.