
Dilations can be performed on a coordinate plane. A dilation can be either an enlargement, which results in an image that is larger than the original figure, or a reduction, which results in an image that is smaller than the original figure.
To perform a dilation on a coordinate plane, you need to know two pieces of information. First, you need to know the scale factor, or magnitude of the enlargement or reduction. Second, you need a center of dilation, or reference point from which the dilation is generated.

![]()
Click on the sketch below to access the interactive and investigate coordinate dilations. Once you have done so, use your experiences to answer the questions that follow.
Perform dilations with a triangle, a rectangle, and a hexagon. Choose relative sizes (scale factors) less than 1 as well as greater than 1. Choose resize points (center of dilation) of the origin, (0, 0), as well as other points in the coordinate plane.
Click to seeInteractive popup. Assistance may be required.
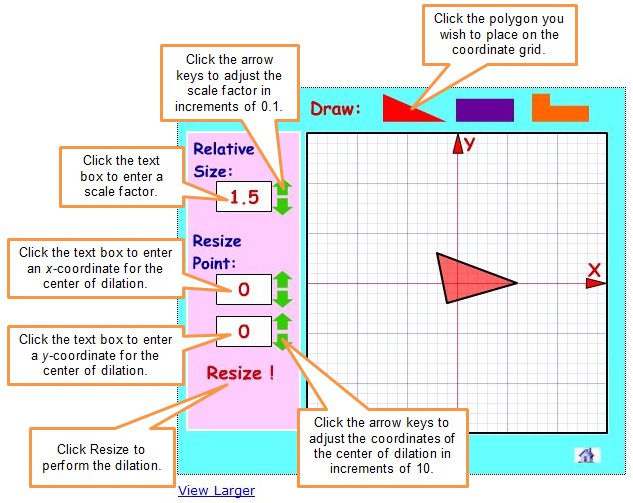
 in using the interactive sketch.
in using the interactive sketch.
| Length of AD | Length of JM | Length of AD over Length of JM Length of AD Length of JM | Scale Factor |
| 1.6 | 3.2 | 3.2 over 1.6 3.2 1.6 = 2 | 2 |
| 1.6 | 4 | 4 over 1.6 4 1.6 = 2.5 | 2.5 |
| 1.6 | 4.8 | 4.8 over 1.6 4.8 1.6 = 3 | 3 |
| 1.6 | 5.6 | 5.6 over 1.6 5.6 1.6 = 3.5 | 3.5 |

What types of scale factor will generate a reduction?
Interactive popup. Assistance may be required.
If the scale factor is between 0 and 1, the dilation will be a reduction.

What types of scale factor will generate an enlargement?
Interactive popup. Assistance may be required.
If the scale factor is greater than 1, the dilation will be an enlargement.

Use the same interactive sketch to complete the following table. Reset the sketch and place the triangle on the coordinate grid. Make sure that the center of dilation is the origin, (0, 0).
Make a copy of the table and paste it into your notes. Fill in the columns for Original Coordinates and Dilated Coordinates.
Original Coordinates |
Scale Factor |
Dilated Coordinates |
|
0.5 |
|
|
0.5 |
|
|
0.5 |
|
|
2 |
|
|
2 |
|
|
2 |
|
Interactive popup. Assistance may be required.
Original Coordinates |
Scale Factor |
Dilated Coordinates |
(−2, 3) |
0.5 |
(−1, 1.5) |
(−1, −2) |
0.5 |
(−0.5, −1) |
(6, 0) |
0.5 |
(3, 0) |
(−2, 3) |
2 |
(−4, 6) |
(−1, −2) |
2 |
(−2, −4) |
(6, 0) |
2 |
(12, 0) |

Use your completed table to answer the questions that follow.
What patterns do you observe in the coordinates?
Interactive popup. Assistance may be required.
The dilated coordinates are equal to the original coordinates multiplied by the scale factor.

How could you express that relationship using an algebraic rule?
Interactive popup. Assistance may be required.
If a polygon is dilated by a scale factor k, the coordinates of each vertex of the polygon are dilated by the following rule:
(x, y) → (kx, ky) 
A triangle has coordinates at S (−4, 3), T (6, 6), and U (4, −2). It is dilated by a scale factor of 3 over 4 3 4 with (0, 0) as the center of dilation.
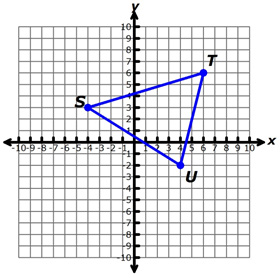
1. What are the coordinates of each vertex after the dilation is performed?
Interactive popup. Assistance may be required. The dilation has a scale factor of 3 over 4 3 4 , which is less than 1, so it will be a reduction. The coordinates of the dilated triangle should all be closer to the origin.  Interactive popup. Assistance may be required. S' (−3, 21 over 4 1 4), T' (41 over 2 1 2,41 over 2 1 2), U' (3, -11 over 2 1 2)
Interactive popup. Assistance may be required. S' (−3, 21 over 4 1 4), T' (41 over 2 1 2,41 over 2 1 2), U' (3, -11 over 2 1 2) 
2. Suppose triangle STU was dialted by a scale factor of 1.5 with the origin as the center of dilation. What would be the coordinates of each vertex of triangle S'T'U'?
Interactive popup. Assistance may be required. The dilation has a scale factor of 1.5, which is greater than 1, so it will be an enlargement. The coordinates of the dilated triangle should all be farther from the origin.  Interactive popup. Assistance may be required. S' (−6, 4.5), T' (9,9), U' (6,−3)
Interactive popup. Assistance may be required. S' (−6, 4.5), T' (9,9), U' (6,−3) 