

In the last section, you investigated how a dilation is used to generate a new figure (image) from an original figure (pre-image). You also saw that the ratios of any pairs of corresponding sides from the dilation were equal. That means the lengths of corresponding sides are proportional, which is one of the attributes of similar figures.
Now that you’ve seen how dilations can be used to generate similar figures, you can use dilations to set up and solve proportions.
Consider the dilation shown below. Trapezoid JKLM is generated by dilating trapezoid ABCD.
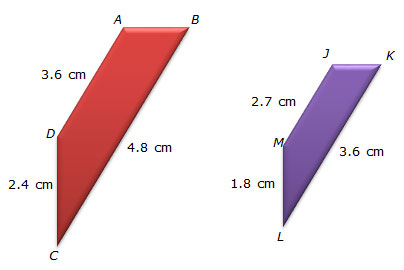
![]() Drag the tiles to set up a proportion that can be used to solve this problem by using the scale factor.
Drag the tiles to set up a proportion that can be used to solve this problem by using the scale factor.
Interactive popup. Assistance may be required.
One way to identify a pair of corresponding sides is to rotate the dilated image so that it has the same orientation as the original preimage. Once the two figures are oriented the same, then you can match the sides that have the same orientation.
Interactive popup. Assistance may be required.
A proportion is a statement that two ratios are equivalent. One way is to write the ratio of the lengths of two corresponding sides. To do this, the side lengths in the numerator of both ratios should be from the same figure. The denominator would be the lengths of the sides that correspond to those of the numerator.
![]() Rotate the image so that it is oriented with the preimage. Then, match the sides of the image with the sides of the preimage.
Rotate the image so that it is oriented with the preimage. Then, match the sides of the image with the sides of the preimage.
3 over 8 3 8 = 12 over x 12 x
3(4) over 8(4) 3(4) 8(4) = 12 over x 12 x
2 over 7 2 7 = x over 21 x 21
2(3) over 7(3) 2(3) 7(3) = 12 over x x 21
Once you have the proportion written, how could you solve the proportion?
Use the figure below to complete the proportions that follow. Quadrilateral MNOP is a dilation of quadrilateral ABCD.
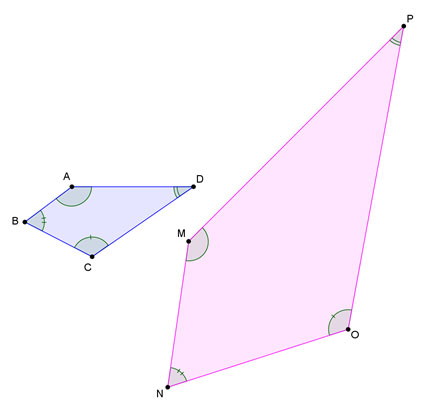
Interactive popup. Assistance may be required.
Identify the angle congruence marks for ∠O and ∠N in quadrilateral MNOP.
Interactive popup. Assistance may be required.
AD over MP AD MP = CB over AB CB ON
Interactive popup. Assistance may be required.
Identify the angle congruence marks for ∠A and ∠B in quadrilateral ABCD.
Interactive popup. Assistance may be required.
AB over MN AB MN = DC over PO DC PO
Interactive popup. Assistance may be required.
Identify the angle congruence marks for ∠A and ∠B in quadrilateral ABCD.
Interactive popup. Assistance may be required.
MN over AB MN AB = NO over BC NO BC