Previously, we worked with square roots and answered the question “What number, when multiplied by itself, gives me the number I started with?”

The square root of a perfect square results in a whole number answer.

Perfect Squares

When finding the square root of a number that is not a perfect square, you will often find an answer that is an irrational number. An irrational number is a number that can’t be written as any fraction and will have a decimal that continues forever with no repeating pattern. Other than square roots, one of the most famous irrational numbers is π, pi, which is about 3.14.

If you have access to a calculator, you can use the square root button, which on most calculators looks like .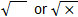

Scott is planting a square garden with an area of 40 square feet.

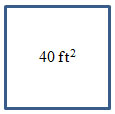
Use a calculator to determine the length of one side of the garden.

(Note, since the decimal repeats, round the number to the hundredths place.)

Check Your Answer

The length of one side is approximately 6.32 feet.

If you don't have a calculator, you will need to estimate the value of the square root.

In the following activity you are going to create the squares. You can change the area of the square by either typing it in the blank or moving the black dot on the line in the upper right hand corner.  

Use the applet to fill in the following table.  Create a square with the area shown in the middle column of the table. Fill in the first column and the last column of the table with the areas of smaller and larger squares as shown on the bottom number line.  

Click to see the completed table

Area of Smaller Square	Area of Square	Area of Larger Square
4	8	9
9	14	16
49	57	64
64	75	81
100	113	121

Based on the information in the table, answer the following questions:

What kind of numbers are the areas of the smaller and larger squares?

Check Your Answer

The areas of the smaller and larger squares are perfect squares.

What does this suggest is a good first step in estimating the value of a square root?

Check Your Answer

Find the perfect squares—one above and one below—that are closest in value to your number.

You are going to use the applet again, but this time you are going to find the square roots of the areas of the squares and write them into the following table in your notes.

Click to see a partially completed table

Smaller Side	Side	Larger Side
2		3
3		4
7		8
8		9
10		11

What should be true of the square root of the area of the side square in each case?

Check Your Answer

It should be between the values for the smaller and larger sides.

Now insert the estimates for the square roots of the areas of the sides.

Click to see the actual square roots

Smaller Side	Side	Larger Side
2	2.8	3
3	3.9	4
7	7.5	8
8	8.7	9
10	10.6	11

How did you decide what the decimal should be?

Check Your Answer

By estimation based on how close the area of the square was to the area of either the smaller or larger square.