In the introduction, you used a balance scale to compare numerical expressions. In this section, you will use a balance scale to model and solve equations.

Consider the equation below.

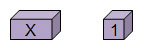
For the balance scale model, use the following figures to represent x and 1. You can represent combinations of x and 1 using combinations of the figures.

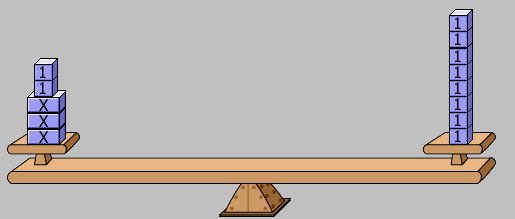
The equation, 2x + 3 = 7, can be built on the balance shown below.

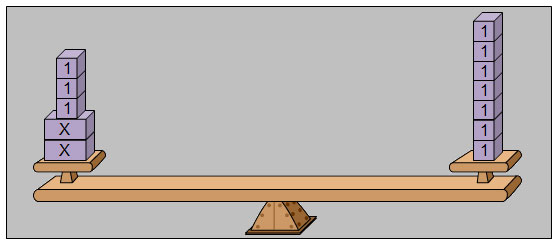
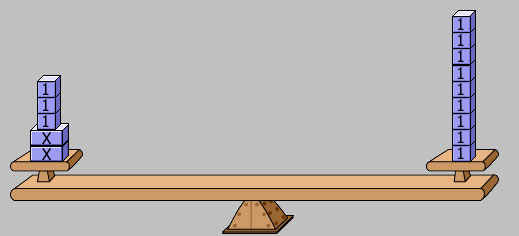
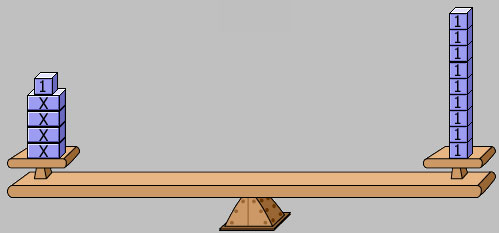
Once the equation is built on the model, the unit blocks, or 1-blocks, can be removed from both sides of the balance to determine the number of unit blocks it takes to balance the 2 x-blocks.

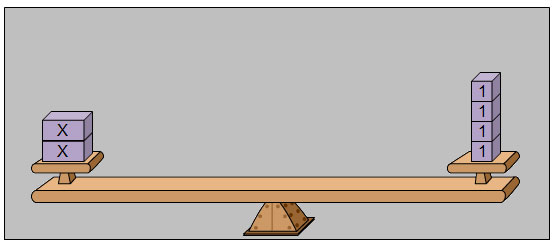
Each x-block must balance the same number of unit blocks, so in this case, each x-block balances 2 unit blocks. According to the model, x = 2.

Watch this equation being solved using the balance model.

Use the interactive below to set up at least 3 equations that will be given to you. The interactive will open in a new browser tab or window. If you need to, click New Problem until you get a two-step equation, or an equation of the form ax + b = c. Use the following steps to help you navigate through the interactive as you set up and solve the given equation.

• Use the x-blocks and unit blocks (1-blocks) to set up the equation.
• Once the equation is correctly set up, click Continue to solve the equation using the balance scale model.
• Identify the operation that needs to be performed to get the x-blocks by themselves on the balance by clicking on the symbol for that operation.
• Enter the number of blocks that need to be added, subtracted, multiplied, or divided.
• Repeat for an additional operation if you need to.

There are directions on the side panel that you can use to step through each equation. If you need additional directions, you can get screen shots using the link below.

Interactive popup. Assistance may be required.

Need additional directions to set up the equation?

Interactive popup. Assistance may be required.

Need additional directions to solve the equation?

Pause and Reflect

An equation of the form ax + b = c, where a, b, and c are numbers and a is not equal to 0, is called a two-step equation. Why do you think these equations are called two-step equations?

Interactive popup. Assistance may be required.

Check Your Answer

Solving these types of equations requires two steps. The first step is to remove b from both sides, and the second step is to divide by a in order to determine the value of x.

How would you solve an equation like 3x − 5 = 10, where b is a negative number?

Interactive popup. Assistance may be required.

Check Your Answer

Instead of subtracting 5 from both sides of the equation, you would need to add 5 to both sides of the equation.

Practice

For questions 1 – 3, use the balance scale to determine the value of x.

1. 3x + 2 = 8
   
   Interactive popup. Assistance may be required.

   Need a hint?

   How many unit blocks do you need to remove from both sides of the model in order to get the 3 x-blocks by themselves?
   Interactive popup. Assistance may be required.

   Check Your Answer

   x = 2
2. 2x + 3 = 9
   
   Interactive popup. Assistance may be required.

   Need a hint?

   How many unit blocks do you need to remove from both sides of the model in order to get the 2 x-blocks by themselves?
   Interactive popup. Assistance may be required.

   Check Your Answer

   x = 3
3. 4x + 1 = 9
   
   Interactive popup. Assistance may be required.

   Need a hint?

   How many unit blocks do you need to remove from both sides of the model in order to get the 4 x-blocks by themselves?
   Interactive popup. Assistance may be required.

   Check Your Answer

   x = 2