Now that you have explored nets of 3-dimensional figures, let's use those nets to generate formulas for surface areas of prisms, pyramids, and cylinders.
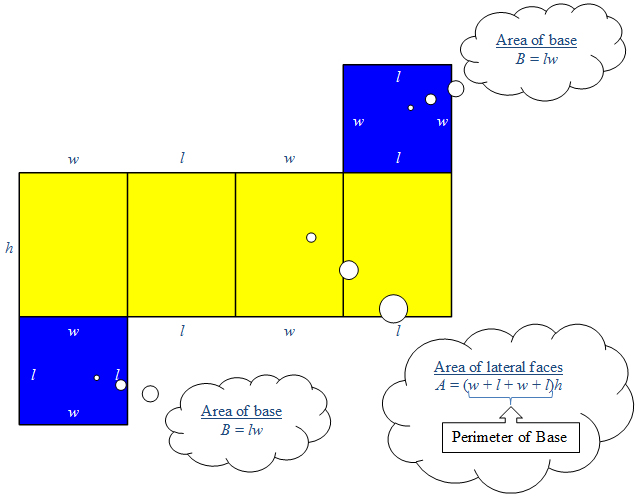
First, consider the net below for a rectangular prism. The bases of the prism are highlighted in blue. We know that the area of a rectangle is the product of the length and the width, so if we label the dimensions of each of the faces of the prism, we can calculate the surface area of the prism.

The diagram shows the lateral faces of the prism forming one big rectangle. The area of the big rectangle is found by adding the widths of all of the individual faces, the perimeter (P) of the prism, and then multiplying by the height.
In other words,
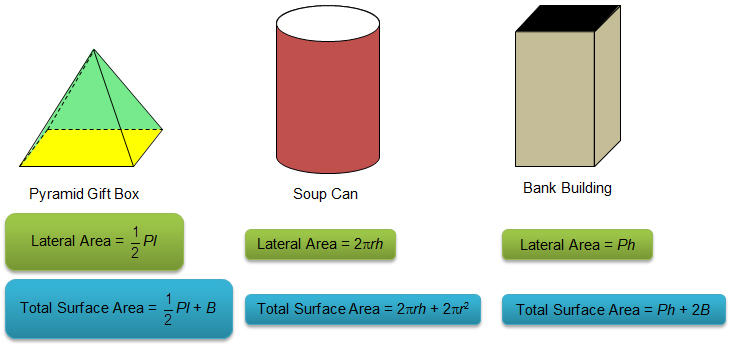
Lateral Area = Perimeter of Base × Height of Prism
Lateral Area = Ph
Next, find the area of one of the two congruent bases, area B. To find the total surface area, add the area of the large rectangle plus two times the area of the base, B.
In other words,
Total Surface Area = Lateral Area + 2 × Area of Base
Lateral Area = Ph + 2B
We can use similar logic for a pyramid.
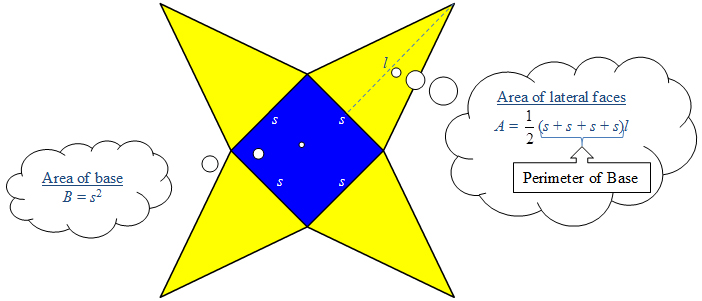
The area of the 4 lateral faces is found by adding the widths of all of the individual faces, the perimeter (P) of the base of the pyramid, and then multiplying by the height of the triangle, which is the slant height, l, of the pyramid.
In other words,
Lateral Area = 1 over 2 1 2 × Perimeter of Base × Slant Height of Pyramid
Lateral Area = 1 over 2 1 2Pl
Next, find the area of the base, area B. To find the total surface area, add the area of the base, B, to the lateral area.
In other words,
Total Surface Area = Lateral Area + Area of Base
Lateral Area = 1 over 2 1 2Pl + B
For a cylinder, we can also develop formulas from the net.
![]()
The dimensions of the lateral surface are the circumference of the circle, 2πr, and the height of the cylinder, h.
In other words,
Lateral Area = Length of Rectangle × Width of Rectangle
Lateral Area = 2πrh
The bases of a cylinder are circles, so we can find the area of a circle using the formula A = πr2.
In other words,
Total Surface Area = Lateral Area + 2 × Area of Base
Total Surface Area = 2πrh + 2πr2

Use the summary chart to drag and drop the formulas to the appropriate 3-dimensional figure.
Being able to determine the surface area of a 3-dimensional figure is an important measurement skill. To determine the surface area, you can calculate the sum of the areas of particular faces or surfaces of a 3-dimensional solid, or use the lateral area and total surface area formulas.
Method 1: Sum of Areas of Faces/Surfaces
If you have a net, it is frequently easier to calculate the area of each figure (polygon or circle), and then add the areas together to get either the lateral area or total surface area.
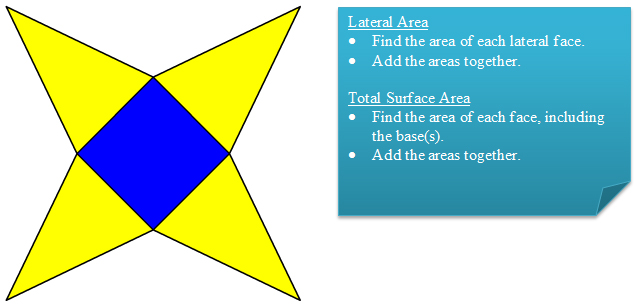
Method 2: Using the Formulas
If you have a figure with dimensions labeled, it may be easier to use the lateral area and surface area formulas.