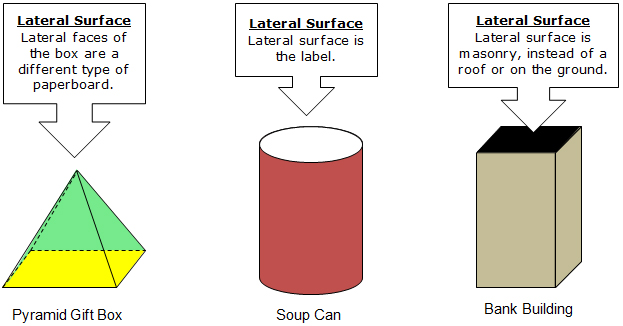
When working with actual 3-dimensional solids, the lateral surface (or surfaces) is oftentimes important in its own right.

In these cases, and many others, it is important to be able to determine the area of only the lateral surface or lateral faces. That area is called the lateral surface area.

Let’s unfold the pyramid gift box to create its net.

Use the dimensions provided to calculate the area of each of the lateral faces of the pyramid. Then calculate the lateral surface area of the pyramid by finding the sum of areas of the lateral faces. Enter the area into the box on each lateral face and the lateral surface area in the box below the figure. Press SUBMIT to check your answers. Incorrect answers will appear in red. Change any incorrect answers, and press SUBMIT again.

Let’s unfold the soup can to create its net.

Use the dimensions provided to calculate the area of the lateral surface of the cylinder. Use 3.14 for π. Enter the area into the box on the lateral surface of the cylinder. Press SUBMIT to check your answers. Incorrect answers will appear in red. Change any incorrect answers, and press SUBMIT again.

Let’s unfold the bank building to create its net.

Use the dimensions provided to calculate the area of each of the lateral faces of the prism. Then calculate the lateral surface area of the prism by finding the sum of areas of the lateral faces. Enter the area into the box on each lateral face and the lateral surface area in the box below the figure. Press SUBMIT to check your answers. Incorrect answers will appear in red. Change any incorrect answers, and press SUBMIT again.

Practice

For each of the nets below, calculate the lateral surface area. Use 3.14 for π.

Cylinder:

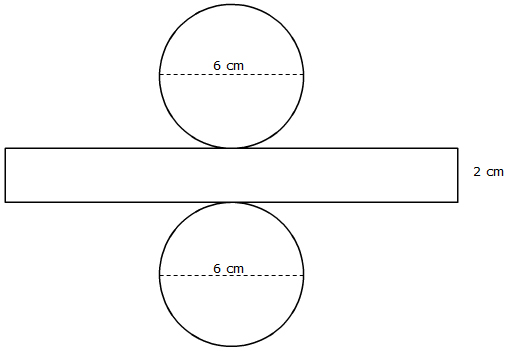
Interactive popup. Assistance may be required. Hint Remember that the length of the lateral surface, which is a rectangle, is equal to the circumference of the circular base. Interactive popup. Assistance may be required. Check Your Answer Lateral Surface Area = Area of Rectangle ≈ (6 cm)(3.14)(2 cm)  = 37.68 square centimeters

Square Pyramid:

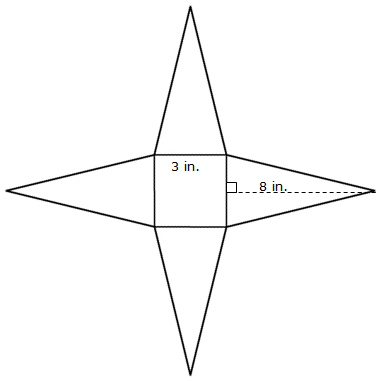
Interactive popup. Assistance may be required. Hint The base of the pyramid is a square, so the lateral faces are the 4 triangles. Use the formula for the area of a triangle. Interactive popup. Assistance may be required. Check Your Answer Lateral Surface Area = 4 × Area of Triangle = 4(1 over 2 1 2)(3 in.)(8 in.) = 48 square inches

Triangular Prism:

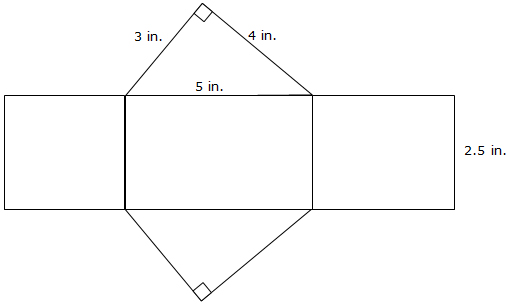
Interactive popup. Assistance may be required. Hint The bases of this prism are the two right triangles. Each of the side lengths of the right triangle corresponds with the length of one of the rectangles that is a lateral face of the prism. Interactive popup. Assistance may be required. Check Your Answer Lateral Surface Area = Sum of Areas of Each Rectangle = (4 in.)(2.5 in.) + (5 in.)(2.5 in.) + (3 in.)(2.5 in.) = 10 + 12.5 + 7.5 = 30 square inches