In the last section, you developed the volume formula for a prism, V = Bh, where B represents the area of the base of the prism, and h represents the height of the prism. You also used the volume formula to solve problems involving rectangular prisms.
However, not all prisms are rectangular prisms. Consider the skyscrapers from different cities that are shown below.
| The Flatiron Building in New York City is a triangular prism since the roof and street outline are congruent right triangles. | The JPMorgan Chase Tower in Houston is a pentagonal prism since the roof and street outline are congruent pentagons. | The Tower in Fort Worth is an octagonal prism since the roof and street outline are congruent octagons. |
 Source: Edificio Fuller (Flatiron) Edit, lmelenchon, Wikimedia Commons |
 |
 Source: The Tower, 500 Throckmorton, Fort Worth, Texas, Magnus Manske, Wikimedia Commons |
In this section, you will focus on triangular prisms, which are prisms with triangular bases.
Use the interactive to create several triangular prisms. Use the dimensions in the interactive to make the calculations to complete the table below. Record the volume of the prism from the interactive. Use the table to answer the questions that follow.
Copy the table below into your notes or a word processing document to enter the data into the table.
| Prism Number | Area of Base | Height of Prism | Volume of Prism |
1 |
6.18 |
5 |
30.9 |
2 |
|||
3 |
|||
4 |
Interactive popup. Assistance may be required.
| Prism Number | Area of Base | Height of Prism | Volume of Prism |
1 |
6.18 |
5 |
30.9 |
2 |
10.98 |
3 |
32.9 |
3 |
2.15 |
8 |
17.2 |
4 |
12.1 |
2 |
24.2 |
Interactive popup. Assistance may be required.
Use the area formula, A = lw over 2 lw 2 , or multiply the length and width of the triangle, and then divide by 2.
Interactive popup. Assistance may be required.
When calculating area, the length and width of the triangle must be perpendicular dimensions. Since the base of the prism is a right triangle, use the two sides that are perpendicular to each other.
Interactive popup. Assistance may be required.
The product of the area of the base and the height of the prism is equal to the volume that is provided in the interactive.
Interactive popup. Assistance may be required.
V = Bh
How is calculating the volume of a triangular prism like calculating the volume of a rectangular prism?
How is calculating the volume of a triangular prism different from calculating the volume of a rectangular prism?
For questions 1 – 3, each composite figure is broken into different component regions. Identify the area formula required to calculate the area of each component region.
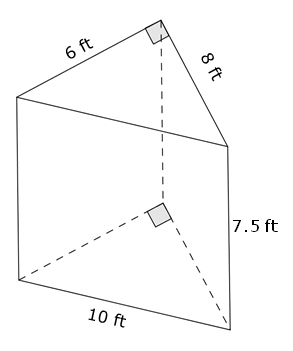
Estimate the volume of air inside the tent that will be air conditioned.
First, round each measurement to the nearest foot.
95 over 8
5
8
rounds to 10 feet.
197 over 8 7 8 rounds to 20 feet.
251 over 8 1 8 rounds to 25 feet.
Next, determine the area of the base, B.
B = lw over 2 lw 2 ≈ (10 ft)(20 ft) over 2 (10 ft)(20 ft) 2 ≈ 100 ft2
Finally, determine the volume of the tent (prism), V.
V = Bh ≈ (100 ft2)(25 ft) ≈ 2,500 ft3
The volume air that will be air conditioned is about 2,500 ft3.
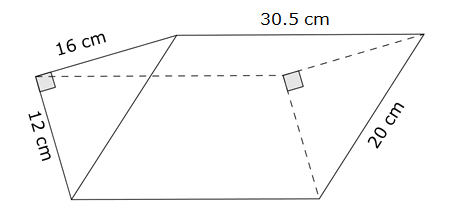
If the entire wedge is melted and poured into bowls that each hold 250 cm3 of cheese, how many bowls can be completely filled with the cheese from the wedge?
First, determine the area of the base, B.
B = lw over 2
lw
2
= (12 cm)(16 cm) over 2
(12 cm)(16 cm)
2
= 96 cm2
Next, determine the volume of the wedge of cheese, V.
V = Bh = (96 cm2)(30.5 cm) = 2,928 cm3
Finally, determine the number of bowls that can be filled with cheese by dividing the volume of cheese by the amount of cheese that each bowl can hold.
2,928 cm3 ÷ 250 cm3 ≈ 11.7
The wedge of cheese can be used to completely fill 11 bowls.
