In the introduction, you reviewed some area formulas that you can use to calculate the area of rectangles or triangles. You also reviewed the volume formula for rectangular prisms.
In this section, you will investigate the volume formula for a rectangular prism more fully, and use the volume formula to solve problems.
![]() Play the interactive animation below to explore the volume formula for rectangular prisms. Use what you see in the animation to answer the questions that follow.
Play the interactive animation below to explore the volume formula for rectangular prisms. Use what you see in the animation to answer the questions that follow.
Interactive popup. Assistance may be required.
12 cubes
Interactive popup. Assistance may be required.
5 layers
Interactive popup. Assistance may be required.
60 cubes
Interactive popup. Assistance may be required.
The number of cubes that it took to completely fill the prism, 60, is the product of the number of cubes in the bottom layer, 12, and the number of layers, 5. In other words, 5 × 12 = 60.
The number of cubes in the bottom layer is the area of the base of the prism, B. The number of layers is the height of the prism, h. Write a formula that relates the volume of the prism, V, to the area of the base of the prism, B, and the height of the prism, h.
A rectangular prism has a base with dimensions 6 centimeters by 8 centimeters and a height of 4 centimeters. What is the volume of the prism?
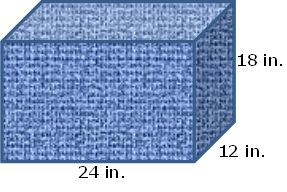
What is the volume of the storage chest?
Interactive popup. Assistance may be required.
Use the formula, V = Bh. Also, notice that the volume is in cubic feet, but the side length is in inches. You will need to convert the inches to feet or cubic feet to cubic inches before performing any calculations.
It may also help to draw a picture.
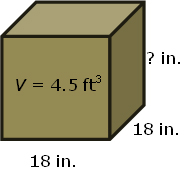

First, convert the side length from 18 inches to feet.
s = 18 in. × 1 ft. over 12 in.
1 ft.
12 in.
= 1.5 ft
Next, determine the area of the base, B.
B = s × s = (1.5 ft)(1.5 ft) = 2.25 ft2
Next, use the volume formula to relate the volume of the prism, V, to the area of the base, B.
V = Bh
4.5 ft3 = (2.25 ft2)(h)
Solve the equation for h.
4.5 ft3 = (2.25 ft2 )(h)
4.5 ft cubed over 2.25 ft squared
4.5 ft3
2.25 ft2
=
2.25 ft. squared times h over 2.25 ft squared
2.25 ft2(h)
2.25 ft2
2 ft = h
The height of the box is 2 feet.

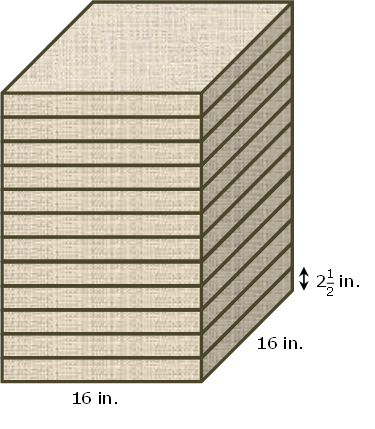
What is the combined volume of the stack of 12 pizza boxes?

First, determine the area of the base, B.
B = lw = (16 in.)(16 in.) = 256 in.2
Next, determine the volume of the prism (one pizza box), V.
V = Bh = (256 in.2)( 21 over 2
1
2
in.) = 640 in.3
Finally, determine the combined volume of the stack of 12 pizza boxes.
V = 12 × 640 in.3 = 7,680 in.3
The volume of the combined stack of pizza boxes is 7,680 in.3.
