Untitled Document

In previous lessons or grades, you may have encountered a four-step problem solving process. Click on each step below.

In this section, you will step through the problem-solving process to solve a problem involving the area of a composite figure. Then, you will practice using the problem-solving process on your own.

Problem

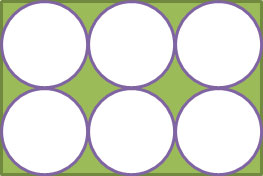
Six circles are used to create an art deco design. The diameter of each circle is 8.5 centimeters, and they are arranged so that they fit exactly inside one rectangle, as shown in the figure below.

What is the approximate area of the green, or shaded region, in the art deco design?

To solve this problem, use the four-step problem-solving model.

Step 1: Read, understand, and interpret the problem.

What information is presented?

Interactive popup. Assistance may be required.
Check Your Answer
The diameter of each circle is 8.5 centimeters.
The six circles create a rectangle that has a width of three circles and a length of two circles.
What is the problem asking you to find?

Interactive popup. Assistance may be required.
Check Your Answer
You are looking for the area of the shaded region, which is inside the rectangle, but outside the circles.
What information do you not need?

Interactive popup. Assistance may be required.
Check Your Answer
There does not appear to be any extra information in the problem.

Step 2: Make a plan.

Draw a picture.

Interactive popup. Assistance may be required.
Check Your Answer
Possible picture:

Step 3: Implement your plan.

What formulas do you need?

Interactive popup. Assistance may be required.
Check Your Answer
Area of a circle: A = πr²

Area of a rectangle: A = lw or A = bh
What information can you interpret from the diagram, table, or other given information?

Interactive popup. Assistance may be required.
Check Your Answer
The length of the rectangle is equal to the combined diameters of two circles. The width of the rectangle is equal to the combined diameters of three circles. To calculate the area of each circle, you need to know the radius, which is half the diameter.
Solve the problem.

Interactive popup. Assistance may be required.
Check Your Answer
Area of Shaded Region = Area of Rectangle − 6 × Area of Circle
Area of Shaded Region = (2 × 8.5 cm)(3 × 8.5 cm) − 6(π)(4.25 cm)²
Area of Shaded Region = (17 cm)(25.5 cm) − 6(π)(18.0625 cm²)
Area of Shaded Region ≈ 433.5 cm2²− 340.30 cm²
Area of Shaded Region ≈ 93.2 cm²

Step 4: Evaluate your answer.

Does your answer make sense?

Interactive popup. Assistance may be required.
Check Your Answer
Yes. The area of one rectangle is about 400 square centimeters, and the area of one circle is about 50 square centimeters. 400 − 6(50) = 100, which is close to the calculated area.
Did you answer the question that was asked?

Interactive popup. Assistance may be required.
Check Your Answer
Yes. The question asked for the area of the shaded region, the area of the rectangle not in the circles.
Are your units correct?

Interactive popup. Assistance may be required.
Check Your Answer
Yes. Area always has square units. Since the original dimensions were in centimeters, the answer should have units of square centimeters.

Pause and Reflect

Why is it important to evaluate your answer?

Interactive popup. Assistance may be required.

Check Your Answer

If you evaluate your answer, then you can have more confidence that your answer is correct.

What are some ways to evaluate your answer?

Interactive popup. Assistance may be required.

Check Your Answer

You can evaluate your answer by rounding the dimensions to estimate your answer. You can also work backwards to make sure that your calculations were performed correctly.

Practice

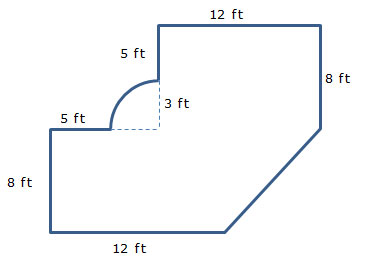
The floor plan for a family room is shown in the figure below.

What is the approximate area of the floor of the living room?

Interactive popup. Assistance may be required.
Need a hint?
Rectangles have four right angles and opposite sides that are congruent. Look for ways to partition the figure around right angles.

Interactive popup. Assistance may be required.
Check Your Answer

Area of Rectangle:
A = bh = (12 ft)(8 ft) = 96 ft²

Area of Quarter Circle:
Calculate the area of the circle, and then divide the area of the circle by 4 to find the area of a quarter circle.
A = πr² ≈ (3.14)(3 ft)² ≈28.26 ft²
A ≈28.26/4 ≈ 7.065 ft²

Area of Trapezoid:
A = 1 over 2 1 2 (b₁ + b₂)h = 1 over 2 1 2 (20 ft + 12 ft)(8 ft) A = 128 ft²

Total Area = Area of Rectangle + Area of Quarter Circle + Area of Trapezoid

Total Area = 96 ft² + 7.065 ft² + 128 ft²
Total Area = 231.065 ft²
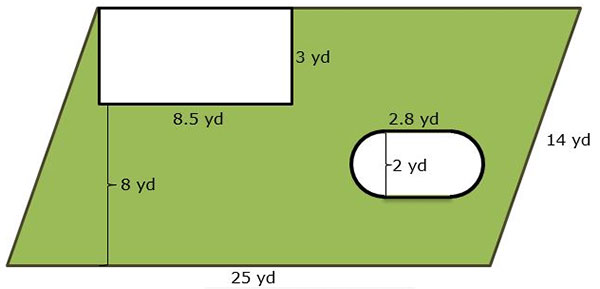
The diagram below shows a pasture that is shaped like a parallelogram. Inside the pasture is a rectangular shed and a trough that is shaped like a rectangle with two semicircles at each end. What is the approximate area of the shaded region, representing the amount of grass available for grazing? Round your answer to the nearest tenth.

Use the grid below to record your answer. Type your answer in the boxes in front of and behind the decimal. Click inside each box to enter the numeral that belongs in the box. Click the bubble beneath the numeral to shade the bubble that matches the numeral. Incorrect portions of your answer will be shaded gray.

Interactive popup. Assistance may be required.
Need a hint?
What is the area of the rectangular shed and the trough made up of two semicircles and one rectangle? What area formulas do you need to use in order to solve this problem?

Interactive popup. Assistance may be required.
Check Your Answer
Possible Solution:
Area of Grazing Land = Area of Pasture − Area of Shed − Area of Trough
Area of Grazing Land = Area of Parallelogram − Area of Rectangle − (Area of Semicircle + Area of Rectangle + Area of Semicircle)

Area of Parallelogram:
A = bh = (25 yd)(8 yd + 3 yd) = (25 yd)(11 yd) = 275 yd²

Area of Rectangle (Shed):
A = bh = (8.5 yd)(3 yd) = 25.5 yd²

Area of Trough:
A = 1 over 2 1 2 πr² + bh + 1 over 2 1 2 πr²
A ≈ 1 over 2 1 2 (3.14)(1 yd)² + (2.8 yd)(2 yd) + 1 over 2 1 2 (3.14)(1 yd)²
A ≈ 1.57 yd² + 5.6 yd² + 1.57 yd²
A ≈ 8.7 yd²

Area of Grazing Land = 275 yd² − 25.5 yd² − 8.7 yd² = 240.8 yd²