In the last section, you practiced different ways to partition a composite figure into rectangles, triangles, parallelograms, trapezoids, squares, circles, semicircles, or quarter circles. In this section, you will take those smaller parts and identify area formulas necessary to calculate the area of each component region of the composite figure.

A swimming pool company offers several designs of swimming pools, including the ones shown below.

swimming pool designs

Interactive exercise. Assistance may be required. Nedra is in charge of calculating the area of the surface of each pool. The animation below shows how Nedra divided the composite figure representing each swimming pool into regions. These regions should have simple area formulas. Click on the Animate button to see how she did it.

Interactive exercise. Assistance may be required. For each of the diagrams, match the formula needed to compute the area for that region. You may use some formulas more than once or not at all.

The actual dimensions for each pool are shown below. Calculate the area of each pool by calculating the area of each component region, and then determine the sum of the areas.

Interactive popup. Assistance may be required.

Check Your Answer - Pool #1

Area of Trapezoid = 1 over 2 1 2 (b1 + b2)h = 1 over 2 1 2 (19.4 + 8)(5.7) = 78.09 ft2
Area of Rectangle = bh = (19.4)(8) = 155.2 ft2
Area of Trapezoid = 1 over 2 1 2 (b1 + b2)h = 1 over 2 1 2 (19.4 + 8)(5.7) = 78.09 ft2
Total Area = 78.09 ft2 + 155.2 ft2 + 78.09 ft2 = 311.38 ft2 Close Pop Up
Interactive popup. Assistance may be required.

Check Your Answer - Pool #2

Area of Semicircle = 1 over 2 1 2 πr2 ≈ 1 over 2 1 2 (3.14)(11)2 ≈ 189.97 ft2
Area of Rectangle = bh = (22)(22) = 484 ft2
Total Area ≈ 189.97 ft2 + 484 ft2 ≈ 673.97 ft2 Close Pop Up
Interactive popup. Assistance may be required.

Check Your Answer - Pool #3

Area of Parallelogram = bh = (18)(12) = 216 ft2
Area of Triangle = 1 over 2 1 2 bh = 1 over 2 1 2 (18)(11) = 99 ft2
Total Area = 216 ft2 + 99 ft2 = 315 ft2 Close Pop Up

Pause and Reflect

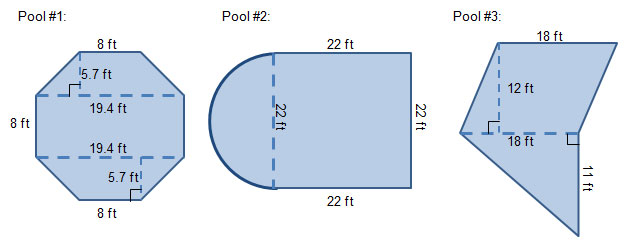
Thinking about area formulas, which type of polygon or circle is it easier to break a composite figure into in order to calculate the area?

Interactive popup. Assistance may be required.

Check Your Answer

Rectangles and parallelograms have the simplest area formulas, A = bh, so their areas are usually easier to calculate.Close Pop Up

Why is it sometimes possible to break a composite figure into different polygons?

Interactive popup. Assistance may be required.

Check Your Answer

Different polygons are related. For example, a trapezoid can also be broken into a rectangle and one or two right triangles, depending on the type of trapezoid. A parallelogram can also be broken into a rectangle and two congruent right triangles.Close Pop Up

Practice

For questions 1 – 3, each composite figure is broken into different component regions. Identify the area formula required to calculate the area of each component region.


  1. Interactive popup. Assistance may be required.

    Need a hint?

    What types of polygons is the composite hexagon broken into? Close Pop Up
    Interactive popup. Assistance may be required.

    Check Your Answer

    Close Pop Up

  2. Interactive popup. Assistance may be required.

    Need a hint?

    What types of polygons is the composite hexagon broken into?Close Pop Up
    Interactive popup. Assistance may be required.

    Check Your Answer

    Close Pop Up

  3. Interactive popup. Assistance may be required.

    Need a hint?

    What types of polygons is the composite hexagon broken into?Close Pop Up
    Interactive popup. Assistance may be required.

    Check Your Answer

    Close Pop Up