
In previous sections, you have defined similarity and used similar figures to identify corresponding parts. With that experience, you are ready to use corresponding sides to solve problems!
Consider the following problem.

![]()
What is another proportion, that Joaquin could use to solve the palm tree problems?

Suppose you had two similar isosceles triangles. What would you know about the base angles, the lengths of the legs of each triangle, and the ratios of the lengths of the corresponding legs?
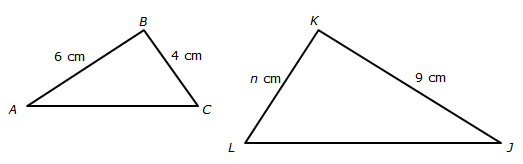
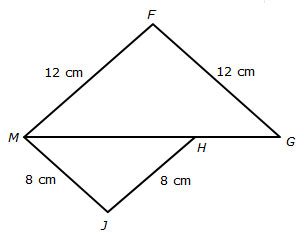
Which of the following statements must be true?
Interactive popup. Assistance may be required.
As you analyze the figure, consider the following questions.
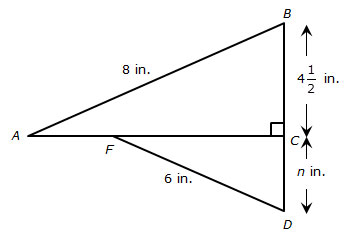
Which of the following statements must be true?
Interactive popup. Assistance may be required.
As you analyze the figure, consider the following questions.