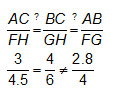Ratios can be used to show a multiplicative relationship between two quantities. When two ratios are equivalent, you can use a proportion to relate the ratios.
Two figures are said to be similar if they are proportionally related. In this section, you will investigate the relationship between corresponding side lengths and corresponding angle measures of similar figures. From that investigation, you will make a formal definition of similar figures.
![]() Use the interactive to begin your investigation of similar figures. In this interactive, triangle ABC and triangle DEF are similar triangles. Use the check boxes to reveal or hide ratios of the lengths of corresponding sides and to reveal or hide the measures of corresponding angles. Move the vertices of triangle ABC around, and pay special attention to patterns in the ratios of the lengths of corresponding sides and to patterns in the measures of corresponding angles. Use the interactive to answer the questions that follow.
Use the interactive to begin your investigation of similar figures. In this interactive, triangle ABC and triangle DEF are similar triangles. Use the check boxes to reveal or hide ratios of the lengths of corresponding sides and to reveal or hide the measures of corresponding angles. Move the vertices of triangle ABC around, and pay special attention to patterns in the ratios of the lengths of corresponding sides and to patterns in the measures of corresponding angles. Use the interactive to answer the questions that follow.
Click and drag on A, B, or C to adjust the size of triangle ABC.
Click on the Show/Hide Ratios box to show or hide the ratios of the lengths of corresponding sides.
Click on the Show/Hide Angle Measures box to show or hide the angle measures.
Use the interactive to answer the following questions.
Interactive popup. Assistance may be required.
The ratios of the lengths of the corresponding sides of the two triangles are always the same.
Interactive popup. Assistance may be required.
The measures of the corresponding angles of the two triangles are always the same.
Interactive popup. Assistance may be required.
Similar triangles are two triangles for which the ratios of the lengths of all pairs of corresponding sides are equivalent and the measures of all pairs of corresponding angles are equal.
![]()
Interactive popup. Assistance may be required.
Yes, the same relationship is true for quadrilaterals.
Now that you have a definition of similarity, how could you check to see if two figures are similar?
Interactive popup. Assistance may be required.
For each pair of corresponding sides, determine if the ratios of the lengths are equivalent. For each pair of corresponding angles, determine if the measures are equal.
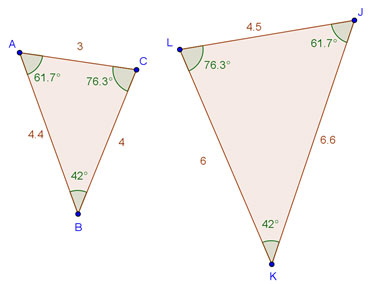
Interactive popup. Assistance may be required.
If the triangles are similar, then all pairs of corresponding sides have lengths that form equivalent ratios, and all pairs of corresponding angles are congruent (that is, they have the same measures).
Interactive popup. Assistance may be required.
Yes, the triangles are similar.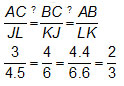

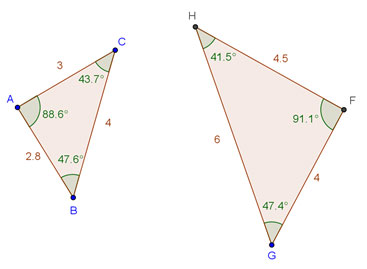

Interactive popup. Assistance may be required.
No, the triangles are not similar.