In the customary measurements of lengths, there are several units that are used, but the inch is the smallest unit of measure.

Copy the table below into your notes.

Fill in the chart below for customary units. Click on the blanks to check your answers.

Similarly, the metric system has several units that are used, but the meter is the most basic unit of measure. Metric prefixes, such as centi- and kilo- are used to indicate larger or smaller units of measure in the metric system.

Copy the table below into your notes.

Fill in the chart below for metric units. Click on the blanks to check your answers.

Consider the following problem situation.

Source: Cycle Race, Mike Baird, Wikimedia

Sean has been training for a bike race. He knows that the race he will be competing in will be 41 kilometers in distance, so he has been riding 25 miles each day in order to train for the race. Have Sean's training rides been at or beyond the distance of the race?

To answer this question, you will need to recall one fact of converting between customary and metric systems: 1 inch = 2.54 cm. Depending on the direction in which you are converting, this fact gives you a rate of conversion as either 1 inch for every 2.54 centimeters or 2.54 centimeters for every inch. Before you answer Sean's question, look at the relationship of 1 inch = 2.54 cm a little more closely.

Specifically, look at the conversion of customary to metric using 1 inch = 2.54 cm. If you had 10 feet and wanted to find out how many meters that would be, you would need to find out how many inches would be in 10 feet. Convert each inch to 2.54 cm. Finally, convert centimeters to meters. Let's examine this process in more detail.

One way to perform unit conversions mathematically is to use a method called dimensional analysis. In dimensional analysis, conversions are represented as unit rates and are positioned such that the numerators and denominators will cancel. Dimensional analysis works because the unit rate is technically the same quantity in both the numerator and denominator, which is equal to 1.

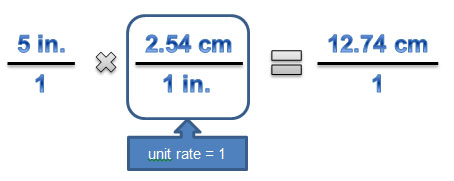
There are many applets that can be used to perform unit conversions.

Watch the video below to see how one math tutor explains the process of using dimensional analysis to convert 10 feet into meters.

Using this same process, let's answer Sean's question.

Sean has been training for a bike race. He knows that the race he will be competing in will be 41 kilometers in distance, so he has been riding 25 miles each day in order to train for the race. Have Sean's training rides been at or beyond the distance of the race?

First, make a plan for converting the units from miles to kilometers.

Interactive popup. Assistance may be required.

Click here to see a possible plan. Knowing that Sean rides 25 miles, you will first need to convert miles into feet, and then feet into inches. This conversion allows you to convert inches into centimeters. Later those centimeters can be converted into meters and finally into kilometers. Then you can compare your answer to the 41 kilometers that was given.

Click on the image below to access the applet. Use the applet to perform dimensional analysis in order to perform the conversion.

Interactive popup. Assistance may be required.

Need additional directions?

After you have finished your conversion and justified your answer, click on the video below to see another student’s solution.

Pause and Reflect

How is dimensional analysis similar to multiplying fractions that have common factors?

Interactive popup. Assistance may be required.

Check Your Answer

In dimensional analysis, the same unit in the numerator and denominator cancels in a similar manner to common factors in numerators and denominators when multiplying fractions.

Why does a common unit in the numerator and in the denominator cancel when using dimensional analysis?

Interactive popup. Assistance may be required.

Check Your Answer

Common units in the numerator and denominator are equal to 1, and anything, except zero, divided by itself is 1.

Practice

1. David Rudisha, from Kenya, set a world record in the men's 800 meter race in August 2010. His time of 1 minute and 41.01 seconds was 0.10 seconds faster than the previous record holder! This race is often called the "half-mile" race here in the United States. What is the distance of this race in miles?
   

   Source: David Rudisha, Erik van Leeuwen, Wikipedia

   Interactive popup. Assistance may be required.

   Need a hint?

   First, convert meters to centimeters, and then use the conversion factor 1 inch = 2.54 centimeters. Once you have inches, you can convert the inches into feet and then feet into miles. Use the conversion factors identified at the beginning of this section of the lesson to help you.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
2. The San Jacinto Monument in Deer Park, Texas, is 567.31 feet tall. The Washington Monument in Washington, DC, is 169 meters tall. How many feet taller is the San Jacinto Monument than the Washington Monument?
   

   Source: Tijuana Brass, San Jacinto Monument, Wikimedia Commons

   Interactive popup. Assistance may be required.

   Need a hint?

   First, convert meters to centimeters, and then use the conversion factor 1 inch = 2.54 centimeters. Once you have inches, you can convert the inches into feet, and determine the difference in the heights of the monuments. Use the conversion factors identified at the beginning of this section of the lesson to help you.
   Interactive popup. Assistance may be required.

   Check Your Answer