One of the ways that we represent problem situations in math is by writing equations.

Proportional relationships are often written as an equation that shows two ratios, written as fractions, equal to each other.

The ratios either show the scale factor used to change one number to another, or the ratios show the constant of proportionality. In the video example in section 1, the first method shows how to use a scale factor to change from 3 lemons to 5 lemons. The video also shows a second method, using the constant of proportionality, that tells you how 1 lemon can be used to make 4 3 cup of lemonade.

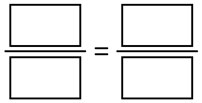
The numbers from your data table will fill in the boxes in a proportion like this:

Here is an example:

Source: Question book-2, AzaToth, Wikimedia Commons

Maria is taking a speed reading class so that she can get her homework done faster. At the end of her class she can read 700 words in 2 minutes. Write a proportion that can be used to solve for the amount of time that it would take her to read 2000 words if she reads at the same speed.

A good first step is to enter all the information from the problem into a table like this one:

 

pages	minutes

Source: Stopwatch2, Hydragyrum,
Wikimedia Commons

 

Copy the table into your notes, and then fill in the given information.

Check Your Answer

pages	minutes
700	2
2000	T

The following animation will place the numbers from the data table into the equation.

Now you try one:

An architect is building a house based on a special scaled diagram called a blueprint. A 2-inch line segment in the diagram represents a 10-foot wall in the actual house. What length line segment would be used to represent a 17- foot wall?

What are two things that are being compared to each other?

Check Your Answer

We are comparing the length of one wall to the length of another.

What changes from one wall to the other?

Check Your Answer

The length of the wall and the length of the line segment in the blueprint both change.

Copy the following table into your notes.

Fill in the empty spaces in the table with information from the problem.

Check Your Answer

length of wall		length of line segment
Wall 1	10 feet	2 inches
Wall 2	17 feet	L

Drag the following data from the problem into the correct spot in the equation.

What rule did you use to correctly fill in the proportional equation?

Check Your Answer

There are two possible rules that you could use:
1. One ratio represented the scale factor to change from a 10 foot wall to a 17 foot wall, and the other ratio applied the same scale factor to a 2 inch line segment.
2. One ratio represented the constant of proportionality (unit rate) that would represent a 10 foot wall with a 2 inch line segment, and the other ratio applied the same constant of proportionality (unit rate) to a 17 foot wall.

Try the interactive again to find a different correct answer. There are many possible correct forms of the equation. The reasons for this are:

1. You can flip both ratios over and the proportion is still valid.
2. The ratios can switch sides of the equal sign and the proportion is still valid.
3. There are two methods to find the correct proportion. The scale factor method and the constant of proportionality (unit rate) method each find valid equations.

Solve your equation for L on a separate piece of paper.

Check Your Answer

To find the final solution we can use any correct form of the equation.

Let's use 10 2 = 17 L .

Take a look at 10 2 . 10 is five times bigger than 2.

The factor used here is 5.

Since the same factor must be used in both ratios, we know that 17 is 5 times L.

Dividing 17 by 5 gives us L = 3.4.

This means that L = 3.4 inches, or a 3.4 inch long line will represent a 17 foot long wall.

Another way to solve this equation is to cross multiply:

17 x 2 = 10 x L

34 = 10L if we divide both sides by 10, we still get 3.4 = L.