In the last section, you used data from a sample to make predictions about the population. In this section, you will use the data presented in graphs to determine if particular conclusions can be made.

Cynthia wanted to know what colors of vehicles the teachers at Northside Middle School drive. So she went to the first row in the teachers’ parking lot and counted the number of different vehicle colors. The data she collected are shown in the bar graph below.

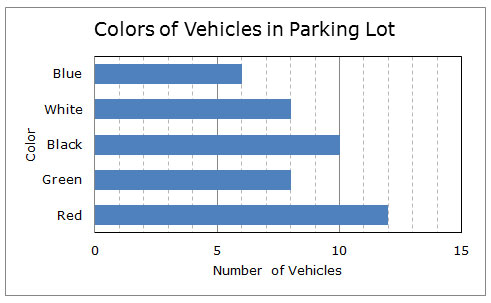
Spin the wheel below to see the conclusions Cynthia made from the data in her graph. Decide if each conclusion is true or false by clicking on the appropriate button. Click “next” to see the next conclusion.

Jacob thought that Cynthia’s car color study was interesting, so he went into the same row of the teachers’ parking lot to look at the age of each car. Jacob determined the car’s age by subtracting the year the car was made from the current year. He represented his data in the dot plot shown below.

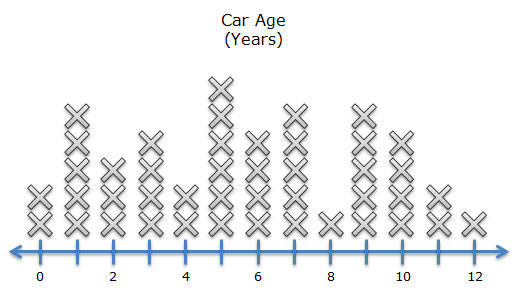
Spin the wheel below to see the conclusions Jacob made from the data in his graph. Decide if each conclusion is true or false by clicking on the appropriate button. Click “next” to see the next conclusion.

Pause and Reflect

How can you use a bar graph to make comparisons of one category compared to the whole set of data represented in the graph?

Interactive popup. Assistance may be required.

Check Your Answer

The length of each bar represents the number of items in a category. The sum of the lengths of the bars represents the number of items in the whole set or sample.

How is a bar graph like a dot plot? How are they different?

Interactive popup. Assistance may be required.

Check Your Answer

Both graphs can be used to represent categorical data. A dot plot can also be used to represent frequencies within a set of numerical data. A bar graph cannot be used for numerical data.

Practice

For questions 1 and 2, the graph below shows how different sources were used to generate electricity in Texas during 2010.

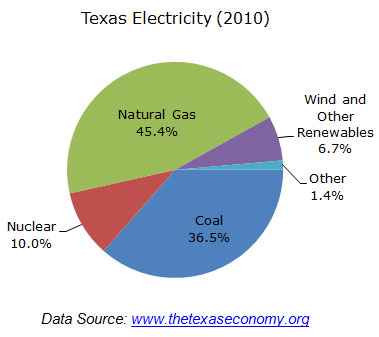
Determine whether or not each of the following statements can be supported from the information in the graph.

1. Natural gas and coal together were used to generate 9 over 10 9 10 of the electricity in Texas in 2010.

   Interactive popup. Assistance may be required.

   Need a hint?

   Determine the total percentage of electricity that was generated using natural gas and coal. Convert the fraction 9 over 10 9 10 to a percent, and compare the two values.
   Interactive popup. Assistance may be required.

   Check Your Answer

   The statement is not supported.
   
   45.4% + 36.5% = 81.9%, so 81.9% of the electricity generated in Texas in 2010 was generated using natural gas or coal. 9 over 10 9 10 is equivalent to 90%. 81.9% < 90%, so this statement is not supported by the information in the graph.
2. Less than a fifth of electricity generated in Texas in 2010 was generated using nuclear energy and wind and other renewable sources.

   Interactive popup. Assistance may be required.

   Need a hint?

   Determine the total percentage of electricity that was generated using nuclear energy and wind and other renewables. Convert the fraction 1 over 5 1 5 to a percent, and compare the two values.
   Interactive popup. Assistance may be required.

   Check Your Answer

   This statement is supported.
   
   10.0% + 6.7% = 16.7%, so 16.7% of the electricity generated in Texas in 2010 was generated using nuclear energy or wind and other renewable sources. 1 over 5 1 5 is equivalent to 20%. 16.7% < 20%, so this statement is supported by the information in the graph.

For questions 3 and 4, the box-and-whiskers plot, or box plot, shown below represents the average monthly low temperatures and high temperatures in San Antonio, Texas.



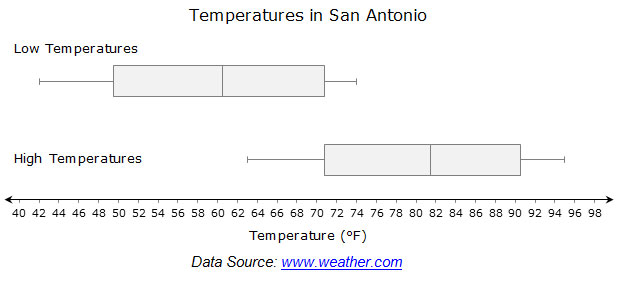
Determine whether or not each of the following statements can be supported from the information in the graph.

3. The median high temperature in San Antonio is approximately 21°F greater than the median low temperature.

   Interactive popup. Assistance may be required.

   Need a hint?

   In a box-and-whiskers plot, or box plot, the vertical line inside the box describes the median of the data set. Use this vertical line, along with the number line, to approximate the median temperature for each data set.
   Interactive popup. Assistance may be required.

   Check Your Answer

   The statement is supported.
   
   The median low temperature is approximately 60.5°F, and the median high temperature is approximately 81.5°F. The difference between these two medians is 21°F.
4. The range of average high temperatures in San Antonio is about 20°F.

   Interactive popup. Assistance may be required.

   Need a hint?

   The range of average high temperatures is indicated by the distance along the number line between the end of each whisker.
   Interactive popup. Assistance may be required.

   Check Your Answer

   The statement is not supported.
   
   According to the graph, the minimum average high temperature is 63°F, and the maximum average high temperature is 95°F. This difference is 32°F. The difference of 20°F represents the interquartile range, or the approximate length of the box in the box-and-whiskers plot.