In the previous two sections, you have investigated situations where two events took place. What happens to the probability if we are only concerned about whether or not a combination of choices could happen? As long as these choices could not happen together, they are called mutually exclusive events. There are shortcuts for determining the probability of these events.
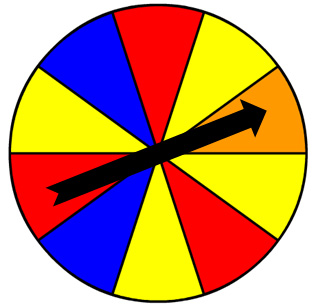
Consider the spinner shown.
Use the spinner to determine the probability of the spinner landing on red, blue, yellow, or orange. Drag the fraction representing this probability to the appropriate place.
The probabilities that you just identified are for the simple event of the spinner being spun once. Suppose, however, that the spinner is spun twice. Because two simple events will occur, these events become compound events.
To determine the probability of a set of mutually exclusive events, we must first identify the probabilities of each of the events occurring by themselves.
Three friends are using the spinner to play a board game. Drag the fraction that represents the probability of each of the following events to the space indicated. For example, for the first line, drag the fraction representing the probability of the spinner landing on yellow to the box in the Probability of First Event column. Drag the fraction representing the probability of the spinner landing on red to the box in the Probability of Second Event column. You may use some fractions more than once or not at all.
Now, calculate the probability of both events occurring for each player by adding the probability of the first event and second event together.
Hot Tip!
The principle that allows us to calculate the probability of two or more mutually exclusive events occurring is also called the Addition Rule and is written as follows:
P(A or B) = P(A) + P(B)
Interactive popup. Assistance may be required.
The probability of Alex spinning yellow or red is equal to (probability of spinning yellow) + (probability of spinning red) = 2 over 5 2 5 + 3 over 10 3 10 = 7 over 10 7 10
The probability of Broderick spinning blue or yellow is equal to (probability of spinning aqua) + (probability of spinning yellow) = 1 over 5 1 5 + 2 over 5 2 5 = 3 over 5 3 5
The probability of Carlos spinning red or blue is equal to (probability of spinning red) + (probability of spinning aqua) = 3 over 10 3 10 + 1 over 5 1 5 = 5 over 10 5 10 = 1 over 2 1 2
Brandy and her sister are playing a card memory game. Brandy wrote the letters shown on index cards.
Brandy will turn the cards over and shuffle them, then randomly draw a card from the pile.
Interactive popup. Assistance may be required.
How many cards contain the letters A, E, I, O, or U?
Interactive popup. Assistance may be required.
P(A) + P(O) + P(E) = 1 over 11
1
11
+ 2 over 11
2
11
+ 1 over 11
1
11
= 4 over 11
4
11
Interactive popup. Assistance may be required.
How many cards contain the letters N or C?
Interactive popup. Assistance may be required.
P(N) + P(C) = 1 over 11
1
11
+ 2 over 11
2
11
= 3 over 11
3
11
Interactive popup. Assistance may be required.
What is the probability of receiving a green gumball? A blue gumball?
Interactive popup. Assistance may be required.
P(green) + P(blue) = 15 over 50 15 50 + 14 over 50 14 50 = 29 over 50 29 50
Interactive popup. Assistance may be required.
What is the probability of receiving a red gumball? A blue gumball?
Interactive popup. Assistance may be required.
P(red) + P(blue) = 21 over 50 21 50 + 14 over 50 14 50 = 35 over 50 35 50 = 7 over 10 7 10