The relationship between multiple events that occur is important. Sometimes, when an event occurs, it does not affect the chances of the next event(s) occurring. For example, when you roll a pair of number cubes, the number that lands on the top face of one number cube does not affect the number that lands on the top of the second number cube.
When there is an independent relationship between two or more events, those events are called independent events.
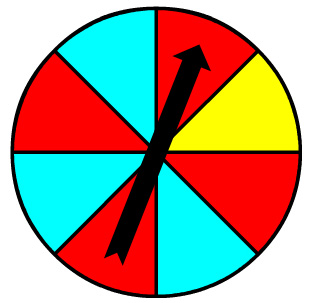
Consider the spinner shown.
Use the spinner to determine the probability of the spinner landing on red, aqua, or yellow. Drag the fraction representing this probability to the appropriate place.
The probabilities that you just identified are for the simple event of the spinner being spun once. Suppose, however, that the spinner is spun twice. Because two simple events will occur, these events become compound events.
You will also notice that the outcomes of these compound events (the spinner being spun twice) are not related to each other. That is, the results of the second spin do not depend on the results of the first spin. Since that is the case, we can call these events independent events.
To determine the probability of a set of independent events, we must first identify the probabilities of each of the events occurring by themselves.
Three friends are using the spinner to play a board game. Drag the fraction that represents the probability of each of the following events to the space indicated. For example, for the first line, drag the fraction representing the probability of the spinner landing on yellow to the box in the Probability of First Event column. Drag the fraction representing the probability of the spinner landing on red to the box in the Probability of Second Event column. You may use some fractions more than once or not at all.
Now, calculate the probability of both events occurring for each player by multiplying the probability of the first event and second event together.
Hot Tip!
The principle that allows us to calculate the probability of two or more events occurring is also called the Multiplication Rule and is written as follows:
P(A and B) = P(A) × P(B)
Interactive popup. Assistance may be required.
The probability of Adriana spinning yellow then red is equal to (probability of spinning yellow) × (probability of spinning red) = 1 over 8 1 8 x 4 over 8 4 8 = 4 over 64 4 64 = 1 over 16 1 16
The probability of Barbara spinning aqua then yellow is equal to (probability of spinning aqua) × (probability of spinning yellow) = 3 over 8 3 8 x 1 over 8 1 8 = 3 over 64 3 64
The probability of Charlene spinning red then aqua is equal to (probability of spinning red) × (probability of spinning aqua) = 4 over 8 4 8 x 3 over 8 3 8 = 12 over 64 12 64 = 3 over 16 3 16
We are also often interested in the probabilities of events resulting from a drawing. If something is drawn, replaced, and then drawn again, the events are independent. This means that the outcome of the second drawing does not depend on the outcome of the first drawing.
Mr. Aimone wrote the names of eight students on slips of paper. He uses the paper slips to randomly draw a student's name to answer questions in his class. After each drawing, Mr. Aimone replaces the slip so that there are always eight slips in the bag. The names of the eight students are as follows:
| Brandon | Chita | Khambrel | Courtney |
| Monica | Thao | Kelsey | Ahmed |
Interactive popup. Assistance may be required.
What is the probability that Brandon’s name will be drawn? Monica’s name?
Interactive popup. Assistance may be required.
1 over 8
1
8
x 1 over 8
1
8
= 1 over 64
1
64
Interactive popup. Assistance may be required.
What is the probability that Khambrel’s name will be drawn? Kelsey’s name?
Interactive popup. Assistance may be required.
1 over 8 1 8 x 1 over 8 1 8 = 1 over 64 1 64
Interactive popup. Assistance may be required.
What is the probability that Courtney’s name will be drawn?
Interactive popup. Assistance may be required.
1 over 8 1 8 x 1 over 8 1 8 = 1 over 64 1 64
A six-sided number cube with each of the numbers 1 through 6 on one face of the cube is rolled.
Interactive popup. Assistance may be required.
What is the probability of rolling a 1? What is the probability of rolling a 5?
Interactive popup. Assistance may be required.
1 over 6 1 6 x 1 over 6 1 6 = 1 over 64 1 36
Interactive popup. Assistance may be required.
What are the numbers on the number cube that are less than 3?
Interactive popup. Assistance may be required.
2 over 6 2 6 = 1 over 3 1 3
Interactive popup. Assistance may be required.
How many numbers on the number cube are even? How many numbers on the number cube are greater than 5?
Interactive popup. Assistance may be required.
3 over 6 3 6 x 1 over 6 1 6 = 3 over 36 3 36 = 1 over 12 1 12