In the last section, you used fractions to write the probability of a simple event. In this section, you will extend that concept to determining the probability of a sequence of independent events occurring.

A bag contains 2 red tiles, 6 green tiles, 1 blue tile, and 3 yellow tiles. Match each simple event with the probability that the event will occur. Drag the probability to the box next to the simple event.

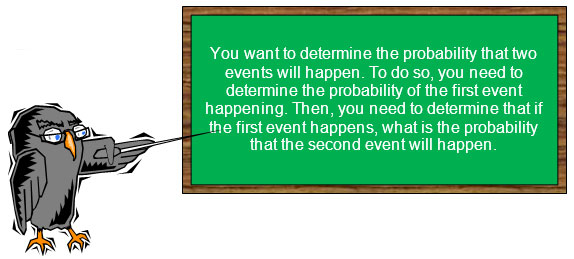
Suppose you want to determine the probability that Jeremy will randomly draw a blue tile, replace the tile, and then draw a yellow tile. Use a Venn diagram to represent the relationship between these two events.

Click View Animation to see how the two events are related.

Pause and Reflect

What operation would you use to find the probability of an event in the intersection of this Venn Diagram?

Interactive popup. Assistance may be required.

Check Your Answer

Use multiplication. With two events, you want to determine what portion of the results where Jeremy draws a blue tile will also include a second drawing of a yellow tile. When you want to determine a fractional part of a quantity, multiplication is the most appropriate operation to use.

Use what you have seen so far to answer the following questions.

• What is the probability that Jeremy will draw a blue tile?

  Interactive popup. Assistance may be required.

  Need a hint?

  Probability is the ratio of the number of ways that Jeremy could draw a blue tile to the number of tiles that Jeremy could draw.
  Interactive popup. Assistance may be required.

  Check Your Answer

  P(blue) = number of blue tiles over total number of tiles Number of Blue Tiles Total Number of Tiles = 1 over 12 1 12
• What is the probability that Jeremy will draw a yellow tile?

  Interactive popup. Assistance may be required.

  Need a hint?

  Probability is the ratio of the number of ways that Jeremy could draw a yellow tile to the number of tiles that Jeremy could draw.
  Interactive popup. Assistance may be required.

  Check Your Answer

  P(yellow) = number of yellow tiles over total number of tiles Number of Yellow Tiles Total Number of Tiles = 3 over 12 3 12 = 3 ÷ 3 over 12 ÷ 3 3 ÷ 3 12 ÷ 3 = 1 over 4 1 4
• What is the probability that Jeremy will draw a blue tile, replace it, and then draw a yellow tile?

  Interactive popup. Assistance may be required.

  Need a hint?

  The probability of both events occurring is the product of the probabilities that each event will occur.
  Interactive popup. Assistance may be required.

  Check Your Answer

  P(blue then yellow) = P(blue) × P(yellow) = 1 over 12 1 12 × 1 over 4 1 4 = 1 over 48 1 48
• Jaden uses the same bag of color tiles as Jeremy. What is the probability that Jaden will draw a red tile, replace it, and then draw another red tile?

  Interactive popup. Assistance may be required.

  Need a hint?

  The probability of both events occurring is the product of the probabilities that each event will occur.
  Interactive popup. Assistance may be required.

  Check Your Answer

  P(red then red) = P(red) × P(red) = 1 over 6 1 6 × 1 over 6 1 6 = 1 over 36 1 36

Practice

1. A bag of letter tiles contains the following tiles.
   
   

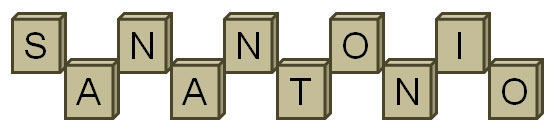
   What is the probability that Bradley will draw a vowel, replace the tile, and then draw another tile with a vowel?

   Interactive popup. Assistance may be required.

   Need a hint?

   These two events, drawing a vowel and drawing a second tile with a vowel, are independent events because Bradley is replacing the first tile. Determine the probability of each event happening, and then find the product of the probabilities.
   Interactive popup. Assistance may be required.

   Check Your Answer

   P(vowel) = number of vowels numbers over total number of tiles Number of Vowels Total Number of Tiles = 5 over 10 5 10 = 5÷5 over 10÷5 5 ÷ 5 10 ÷ 5 = 1 over 2 1 2
   
   P(vowel then vowel) = P(vowel) × P(vowel) = 1 over 2 1 2 × 1 over 2 1 2 = 1 over 4 1 4
2. A bag contains 3 red marbles, 2 green marbles, and 5 yellow marbles. What is the probability that Xuan will draw a green marble, replace it, and then draw a yellow marble?

   Interactive popup. Assistance may be required.

   Need a hint?

   These two events, drawing a green marble and drawing a yellow marble, are independent events because Xuan is replacing the first marble. Determine the probability of each event happening, and then find the product of the probabilities.
   Interactive popup. Assistance may be required.

   Check Your Answer

   P(green) = number of green marblbes over total number of marbles Number of Green Marbles Total Number of Marbles = 2 over 10 2 10 = 2÷2 over 10÷2 2 ÷ 2 10 ÷ 2 = 1 over 5 1 5
   
   P(yellow) = number of yellow marbles over total number of marbles Number of Yellow Marbles Total Number of Marbles = 5 over 10 5 10 = 5÷5 over 10÷5 5 ÷ 5 10 ÷ 5 = 1 over 2 1 2
   
   P(green then yellow) = P(green) × P(yellow) = 1 over 5 1 5 × 1 over 2 1 2 = 1 over 10 1 10
3. A random number generator is used to randomly select 2 numbers between 1 and 10, and repetition of a number is allowed. What is the probability that the first number selected is prime and the second number selected is greater than 7?

   Interactive popup. Assistance may be required.

   Need a hint?

   These two events, selecting a prime number and then selecting a number greater than 7, are independent events because repetition of a number is allowed. Determine the probability of each event happening, and then find the product of the probabilities.
   Interactive popup. Assistance may be required.

   Check Your Answer

   P(prime) = number of prime numbers over total number of numbers Number of Prime Numbers Total Number of Numbers = 4 over 10 4 10 = 4÷2 over 10÷2 4 ÷ 2 10 ÷ 2 = 2 over 5 2 5
   
   P(greater than 7) = number of prime numbers over total number of numbers Number of Numbers Greater than 7 Total Number of Numbers = 3 over 10 3 10
   
   P(prime then greater than 7) = P(prime) × P(greater than 7) = 2 over 5 2 5 × 3 over 10 3 10 = 6 over 50 6 50 = 6÷2 over 50÷2 6 ÷ 2 50 ÷ 2 = 3 over 25 3 25