In this section, you will look at models to represent multiplying and dividing fractions.

Multiplying Fractions

Use the interactive below to represent the problem and graphically illustrate the product. Use the Numerator and Denominator sliders to create each fraction or mixed number. You may also need to use the Zoom in/out sliders to see the entire model.

Interactive popup. Assistance may be required.

Need additional directions?

Use the interactive to answer the following questions:

• What are the dimensions of the shaded rectangle in the solution?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The dimensions are 3 over 4 3 4 by 61 over 21 2 .

• The solid lines represent the boundaries of a rectangle with an area of 1 square unit. The dashed lines represent the boundaries of a number of equal-sized regions within this area. What fraction of 1 does each smaller rectangle represent?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Since there are 8 of these regions inside a rectangle with an area of 1 square unit, each region represents 1 over 8 1 8 .

• Beginning with the right-hand side of the shaded region shown below, imagine moving the rectangles from the right-hand side of the shaded region shown below to the left-hand side until you fill up each unit square.
  
  

  When you have filled up all of the unit squares that you can, what would the shaded region look like?

  Interactive popup. Assistance may be required.

  Check Your Answer

  
• What mixed number does this rearranged figure represent? How does this compare with the product of 3 over 4 3 4 and 61 over 21 2 ?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The rearranged figure represents 47 over 87 8 , which is the same as the product of 3 over 4 3 4 and 61 over 21 2 .

Dividing Fractions

• Barbara knew this was a division problem, not a multiplication problem. How did she know that?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Barbara recognized that she was partitioning an object into equally-sized pieces. This action indicates the operation of division.

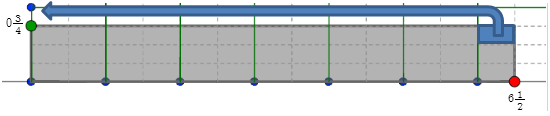
To solve this problem, Barbara used a fraction strip generator, which gave her the following diagram.




• Use the diagram to explain why the quotient of 61 over 21 2 ÷ 1 over 2 1 2 is 13.

  Interactive popup. Assistance may be required.

  Check Your Answer

  This division problem is essentially asking, "How many pieces of 1 over 2 1 2 are there in 61 over 21 2 ?" To determine the solution, count the number of pieces that have a length of 1 over 2 1 2 inch that will fit, end to end in order to make a length of 61 over 21 2 inches.

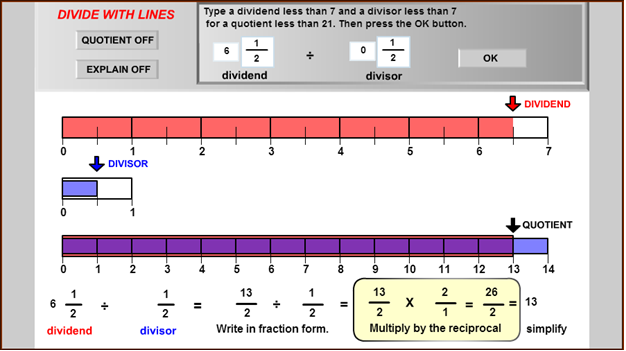
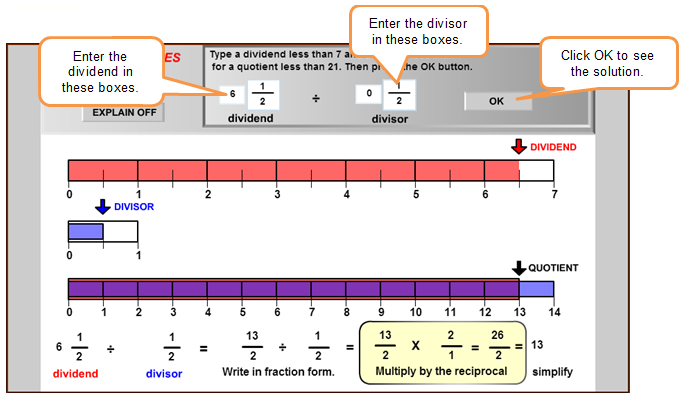
Use the same fraction strip generator that Barbara used to solve the problem below.

Click the image below to open the fraction strip generator in a new web browser tab or window. Enter the key information from the problem, including the dividend and the divisor, and then use the results to answer the questions that follow.

Interactive popup. Assistance may be required.

Need additional directions?

• In the fraction diagrams, both 53 over 434 and 3 over 8 3 8 are marked off into eighths. Why do you think that is the case?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Division works with grouping, and you need to know how many groups of 3 over 8 3 8 there are in 53 over 43 4 .

• To divide 53 over 434 by 3 over 8 3 8 , the number sentence beneath the diagrams shows multiplication of 53 over 43 4 by 8 over 3 8 3 , which is the reciprocal of 8 over 3 3 8 . Multiplying by 8 over 3 8 3 is the same as multiplying by 8 and then dividing by 3. Why do you need to multiply 53 over 43 4 by 8, which is the numerator of the reciprocal?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The dividend needs to be multiplied by 8 because you need to know how many eighths are in 53 over 4 3 4 . This information is important because the eighths will be grouped in the next step of the algorithm.

• The next step in the number sentence divides the product of 53 over 4 3 4 and 8 by 3 (multiplies 53 over 4 3 4 by the fraction, 8 over 3 8 3 ). Why do you need to divide by 3 at this point?

  Interactive popup. Assistance may be required.

  Check Your Answer

  You need to divide by 3 because for division, you need to count how many groups of 3 over 8 3 8 there are in 53 over 4 3 4 .

See the completed fraction diagram for Patrice’s ornament problem.

Interactive popup. Assistance may be required.

Completed fraction diagram

Pause and Reflect

How does the multiplication algorithm connect to the area model that you used in the first interactive?

Interactive popup. Assistance may be required.

Check Your Answer

The area model has the dimensions of each factor in the multiplication sentence. Each unit is broken into the number of parts that is equal to the product of the denominators. The number of rows and columns of these smaller regions is determined by the numerators.

How does the division algorithm connect to the fraction strip model that you used in the interactive?

Interactive popup. Assistance may be required.

Check Your Answer

The fraction strip model allows you to mark off the units according to the denominator of the divisor, and then count the number of groups equal to the numerator of the divisor.

Practice

1. Suzanne wants to paint a mural on a rectangular wall that is 125 over 8 5 8 feet long and 81 over 2 1 2 feet high. What is the area of the wall on which Suzanne will paint the mural?

   Interactive popup. Assistance may be required.

   Need a hint?

   How do you determine the area of a rectangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   125 over 8 5 8 × 81 over 212 = 101 over 8 101 8 × 17 over 2 17 2 = 1717 over 16 1717 16 = 1075 over 165 16
   
   The area of the wall is 1075 over 165 16 square feet.
2. Martina can run 181 over 2 1 2 miles in 17 over 8 7 8 hours. How many miles per hour can Martina run?

   Interactive popup. Assistance may be required.

   Need a hint?

   Since this question is asking you to determine a rate, use division.
   Interactive popup. Assistance may be required.

   Check Your Answer

   181 over 2 1 2 ÷ 17 over 878 = 37 over 2 37 2 ÷ 15 over 8 15 8 = 37 over 2 37 2 × 8 over 15 8 15 = 296 over 30 296 30 = 913 over 1513 15
   
   Martina can run 913 over 1513 15 miles per hour.
3. After a cold front passed through, the temperature fell at a rate of 41 over 212 °F per hour. After 51 over 212 hours, what was the change in temperature?

   Interactive popup. Assistance may be required.

   Need a hint?

   What sign would you use to indicate a decreasing temperature?
   Interactive popup. Assistance may be required.

   Check Your Answer

   -41 over 2 1 2 × 51 over 212 = 9 over 2- 9 2 × 11 over 2 11 2 = 99 over 4- 99 4 = -243 over 43 4
   
   The change in temperature was −243 over 4 3 4 °F.