Equations are number sentences showing two numbers or expressions that are equivalent. If one expression has a variable, then you can solve that equation to determine the value of the variable.

Source: Toby Hudson, Brass scales with flat trays balanced, Wikimedia Commons

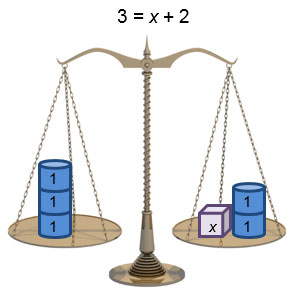
In a previous lesson, you saw how a balance scale could be used to show two expressions that are equivalent. In the figure shown, the scale is balanced because the expression x + 2 is equivalent to 3.

Source: 2cv4 Automobile Car, Webmichl, Open Clipart

Equations can be used to represent problem situations. For example, Marcy purchased 5 toy cars at $3.25 each. How much money, y, did Marcy spend, excluding sales tax?

You can represent Marcy’s purchase with an equation. To do so, you must first recognize the operation being used to calculate the total amount of money that Marcy spent.

In this lesson, you will investigate different ways to determine a mathematical operation that best represents an action being taken in a problem situation. In doing so, you will learn how to write equations to represent those situations. You will also learn how to write problem situations from an equation by connecting real-world actions to the operation represented in the equation.