In the previous sections, you used the commutative and associative properties of addition and multiplication to determine whether or not two expressions are equivalent. In this section, you will investigate an additional property that you can use to determine if two expressions are equivalent.

Use the interactive below to determine whether or not the given expressions are equivalent. Record your results in a table like the one shown. Click the Next button to see the next pair of expressions.

Copy the following table into a word processing or spreadsheet app or program. Use the results from the interactive to complete the table.

Interactive popup. Assistance may be required.

Check Your Answer

Expression 1	Expression 2	Equivalent? (Yes/No)
2(x + 3)	2x + 6	Yes
3(1 + 2x)	3 + 6x	Yes
4(x + 1)	4x + 1	No
3x − 6	3(x − 6)	No
2x − 8	2(x − 4)	Yes

Use your completed table and the interactive to answer the questions that follow.

• Look at the expressions with a number in front of parentheses. When that number is multiplied by both terms inside parentheses, is the resulting expression equivalent to the original expressions? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Yes, the two expressions are equivalent because the scale is balanced and the scale contains the same number of each block on both sides.

• Look at the expressions with a number in front of parentheses. When that number is multiplied by only one term inside parentheses, is the resulting expression equivalent to the original expressions? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  No, the two expressions are not equivalent because the scale is not balanced and the scale contains different numbers of each block on each side.

• Is 24 ÷ (4 + 6) equivalent to (24 ÷ 4) + (24 ÷ 6)? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  No. If you follow the order of operations in the first expression, you add 4 + 6 first to get 10, and then divide 24 by 10 to get 2.4. In the second expression, you perform the division inside parentheses first to get (6) + (4), and then simplify 6 + 4 = 10. Both expressions simplify to different numbers.
  24 ÷ (4 + 6) = 24 ÷ (10) = 2.4
  (24 ÷ 4) + (24 ÷ 6) = (6) + (4) = 10

• Is (16 + 12) ÷ 4 equivalent to (16 ÷ 4) + (12 ÷ 4)? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Yes. If you follow the order of operations in the first expression, you add 16 + 12 first to get 28, and then divide 28 by 4 to get 7. In the second expression, you perform the division inside parentheses first to get (4) + (3), and then simplify 4 + 3 = 7. Both expressions simplify to the same number.
  (16 + 12) ÷ 4 = (28) ÷ 4 = 7
  (16 ÷ 4) + (12 ÷ 4) = (4) + (3) = 7

Pause and Reflect

The distributive property of equality states that the product of a quantity and a sum of two addends is equal to the sum of the product of the quantity and each addend. For which combinations of operations does the distributive property hold true?

Interactive popup. Assistance may be required.

Check Your Answer

The distributive property is true multiplication over addition, multiplication over subtraction. The distributive property only works if the sum or difference (inside parentheses) is the dividend, not the divisor.

Generalize the distributive property using the numbers a, b, and c.

Interactive popup. Assistance may be required.

Check Your Answer

Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
ab + ac = a(b + c)

Distributive Property of Multiplication over Subtraction:
a(b − c) = ab − ac
ab − ac = a(b − c)

Distributive Property of Division over Addition:
(a + b) ÷ c = (a ÷ c) + (b ÷ c)

Distributive Property of Division over Subtraction:
(a − b) ÷ c = (a ÷ c) − (b ÷ c)

Practice

1. Which of the following pairs of expressions are equivalent?
   1. 3(n − 5) and 3n − 15
   2. 0.5(3z + 10) and 1.5z + 10
   3. 4j − 10 and 4(j − 2.5)
   4. -6m − 18 and -6(m − 3)
   Interactive popup. Assistance may be required.

   Need a hint?

   The associative property of equality is true only for addition and multiplication.
   Interactive popup. Assistance may be required.

   Check Your Answer

   I and III only
   For expression II, the factor of 0.5 was multiplied by 3z but not by 10.
   For expression IV, -6(-3) = 18, not -18.
2. Jeannie modeled an expression using algebra tiles. The expression she modeled is shown below.
   

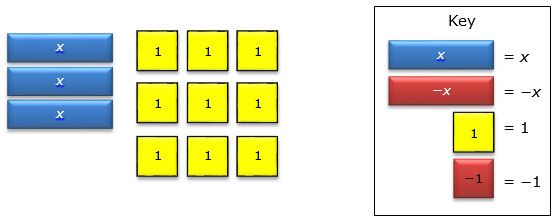
   Jeannie’s friend, Antonio, said that Jeannie modeled the expression 3(x + 3). Is Antonio correct? Explain.

   Interactive popup. Assistance may be required.

   Need a hint?

   To model the distributive property, arrange the tiles in groups that have the same number and type of tile in each group.
   Interactive popup. Assistance may be required.

   Check Your Answer

   Yes. Jeannie modeled 3x + 9, which is equivalent to 3(x + 3) by the distributive property.
3. Three students wrote an expression to describe the perimeter of the rectangle below.
   

   Which students wrote equivalent expressions?

   Interactive popup. Assistance may be required.

   Need a hint?

   The perimeter of a rectangle can be found using the formula, P = 2l + 2w
   Interactive popup. Assistance may be required.

   Check Your Answer

   Nina and Olivia have equivalent expressions.
   The perimeter of the rectangle is 2(5m − 1) + 2(3) = 2(5m) − 2(1) + 2(3) = 10m − 2 + 6 = 10m + 4, which is the same as Nina’s expression.
   Using the distributive property for Michelle’s expression:
   2(5m − 1) − 6 = 2(5m) − 2(1) − 6 = 10m − 2 − 6 = 10m − 8. This expression is not equivalent to Nina’s or Olivia’s.