In the previous section, you used models to multiply fractions that were less than 1 and formalized an algorithm, or process, that you can use to multiply two fractions without a model. But what happens when one or more of the factors is a fraction greater than 1? In this part of the lesson, you will investigate an area model used to multiply mixed numbers.
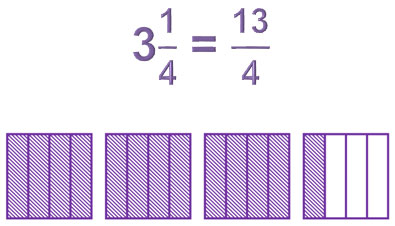
Recall that you can write a fraction greater than 1 as either a mixed number or an improper fraction. For example, the model below shows how 31 over 4 1 4 is equivalent to 13 over 4 13 4 .
If you would like, you can explore how to rewrite other mixed numbers as improper fractions. Click the image below to open the interactive in a new web browser tab or window. Use the sliders to change the numerator and denominator for an improper fraction and see the resulting mixed number.
How can you convert a mixed number to an improper fraction without using a model?
Now that you have reviewed how to write mixed numbers as improper fractions, you can use that skill to help you multiply mixed numbers. Consider the problem below.
You can use an area model to set up and solve this problem. To do so, let each factor represent one dimension of a rectangle. In this case, one dimension will be 13 over 5 3 5 and the other dimension will be 21 over 5 1 5 .
Click the image below to open the interactive to investigate the area model of multiplying mixed numbers. The interactive will open in a new web browser tab or window. In the interactive, use the solution method slider to see two different ways that the area model could be used to solve this multiplication problem. Use the interactive to answer the questions that follow.
Use what you noticed in the interactive to answer the following questions.
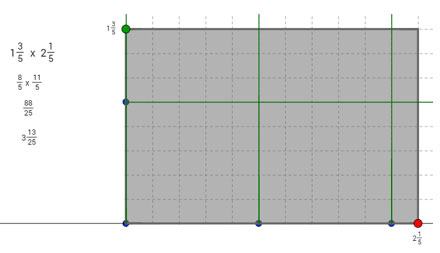
In the multiplication problem 13 over 5 3 5 × 21 over 5 1 5 , one solution method is shown in the diagram below.
Interactive popup. Assistance may be required.
25, which is equal to the product of the denominators of the two factors.
Interactive popup. Assistance may be required.
88, which is equal to the product of the numerators of the two factors when written as improper fractions.
Interactive popup. Assistance may be required.
If both factors are written as improper fractions, multiply them as you would for fractions less than 1. The numerator of the product is the product of the numerators of the factors, and the denominator of the product is the product of the denominators of the factors. Simplify or reduce the fraction, including writing it as a mixed number, if necessary.
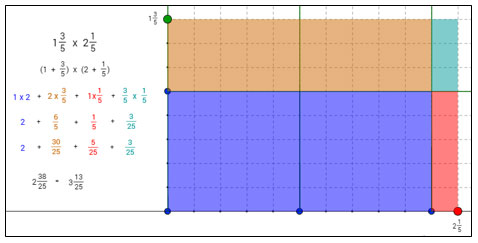
Another way to represent the solution to the multiplication problem 13 over 5 3 5 × 21 over 5 1 5 is shown in the diagram below.
Interactive popup. Assistance may be required.
1 × 2 represents the product of the whole number parts of each factor.
Interactive popup. Assistance may be required.
The denominator of each partial product is equal to the number of parts into which a whole square unit is broken (25). This number is the same as the product of the denominators of the original factors (5 × 5 = 25).
Interactive popup. Assistance may be required.
The numerator is the number of shaded parts from multiplying one of the two parts of each mixed number.
In this section, you saw two different methods of multiplying mixed numbers being represented in an area model. How does the first method (convert mixed numbers to improper fractions) compare to the second method (partial products)?
Interactive popup. Assistance may be required.
Choose one of two methods: convert each mixed number to an improper fraction and multiply the fractions, or determine the partial products and add the four partial products together.
Interactive popup. Assistance may be required.
Multiply 13 over 4 3 4 by 81 over 2 1 2
Interactive popup. Assistance may be required.
To calculate the area of a rectangle, use the formula A = lw.
