In the previous section, you found the data’s center. In this section, you will look at the entire spread of the data. When interpreting data, the spread of the data is as important as the center. The range tells us how far apart the data is. The interquartile range or IQR tells us information around the median or center of the data and functions as a means to eliminate outliers that would be included in the range.

Click on the clipboard to review the definitions.

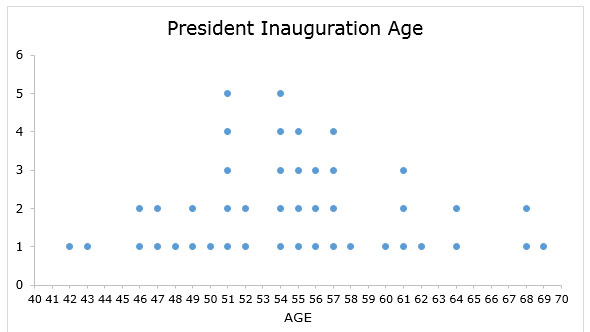
Use the clipboard and the dot plot below to answer the following questions. In the previous section, you saw that the mean and median for the ages of the US Presidents when they were inaugurated (54.72 and 54.5). Below is the same dot plot.

Remember, the U.S. Constitution decrees that the president must be at least 35 years old.

• Compare the mean and the median for this data set.

  Interactive popup. Assistance may be required.

  Need a hint?

  Read the definitions on the clipboard, and discern the difference by using an example from data given.
  Interactive popup. Assistance may be required.

  Check Your Answer

  The mean is the average; it does not have to be exactly in the middle because it is a value that represents the entire graph. In the example, 54.72 is the mean. The median is the number exactly in the middle of a sorted set of data. In the example, 54.5 is the median. In this case they are close, but they are not the same.
• What was the age of the youngest president? Do you know who the youngest president was?

  Interactive popup. Assistance may be required.

  Need a hint?

  The youngest president would be represented as the dot on the plot that is farthest to the left.
  Interactive popup. Assistance may be required.

  Check Your Answer

  Theodore Roosevelt was 42, and the youngest president to hold office following the assassination of William McKinley; John F. Kennedy, 43, was the youngest elected president.
• What was the age of the oldest president, and do you know who he was?

  Interactive popup. Assistance may be required.

  Need a hint?

  The oldest president would be represented as the dot on the dot plot the farthest to the right.
  Interactive popup. Assistance may be required.

  Check Your Answer

  Ronald Reagan was 69 at his inauguration; he was the oldest inaugurated president and the oldest president to leave the office.
• The range of the inaugural ages of the US Presidents is the difference between the oldest and the youngest. Find the range of inaugural ages.

  Interactive popup. Assistance may be required.

  Need a hint?

  Subtract the age of the youngest from the age of the oldest president.
  Interactive popup. Assistance may be required.

  Check Your Answer

  69 − 42 = 27
  The range of the inaugural ages of the presidents is 27.

The Interquartile Range

The interquartile range is a measure of where the middle half of the data is located. The information provided by the interquartile range will exclude outliers and may give a more accurate picture of the information.

To practice finding the interquartile range, use the 10 question assessment scores from Mr. Smith’s fourth period ELA class, located at the beginning of section 2.

The students’ assessment scores are as follows.

70, 60, 80, 90, 50, 100, 80, 90, 80, 70, 50, 90, 100, 90, 80, 70, 70, 80, 90, 80, 100, 100, 70, 80, 80

Follow the steps below to find the interquartile range of the assessment scores.

Use the information from the interactive about interquartile range to answer the following:

• Find the interquartile range of the following data.

  14, 19, 23, 12, 15, 18, 15, 16, 15, 16, 17, 14

  Interactive popup. Assistance may be required.

  Need a hint?

  First, put the numbers in order from smallest to largest, and then follow the steps detailed in the interactive.
  Interactive popup. Assistance may be required.

  Check Your Answer

  Put the numbers in order from smallest to largest: 12, 14, 14, 15, 15, 15, 16, 16, 17, 18, 19, 23
  
  Find the median: 12, 14, 14, 15, 15, 15, 16, 16, 17, 18, 19, 23
                    15 + 16 = 31
                    31 ÷ 2 = 15.5 − Median
  
  Group the two sets of numbers.
  
  12, 14, 14, 15, 15,
  16, 17, 18, 19, 23
  
  Find the middle of each group: 14 and 18.
  
  12, 14, 14, 15, 15,
  16, 17, 18, 19, 23
  
  Subtract Q3 − Q1 = 18 − 14 = 4.
  The interquartile range is 4.

Practice

A fascinating age group made popular by the television show “Shark Tank” is a group of young people who became millionaires before they reached the age of 20. Below is a box plot and a histogram depicting the ages of young millionaires.

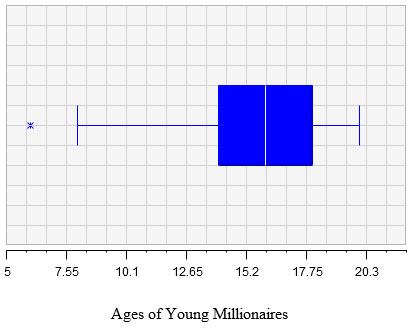
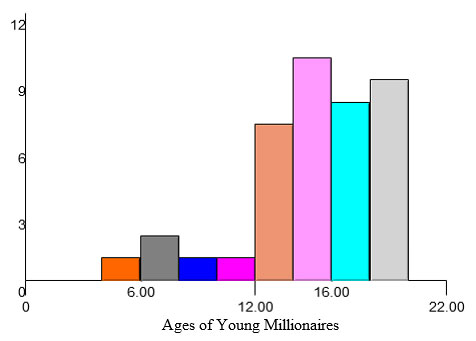
Use the graphs to answer the following questions:

1. Find the range of ages of young millionaires.

   Interactive popup. Assistance may be required.

   Need a hint?

   First, find the age of the youngest millionaire which is the age farthest to the left, and then find the age of the oldest millionaire which is the age farthest to the right. Next, subtract the ages.
   Interactive popup. Assistance may be required.

   Check Your Answer

   The youngest is 6, and the oldest is 20. To find the range, subtract the youngest age from the oldest age: 20 − 6 = 14. The spread is 14 years.
2. Find the median.

   Interactive popup. Assistance may be required.

   Need a hint?

   The median is the number in the middle. Since there are only a few very young millionaires, the median would be closer to the right.
   Interactive popup. Assistance may be required.

   Check Your Answer

   Looking at the histogram, the median is probably around 16 since there are a large number of millionaires after 16 that balance the number of young millionaires before 16.
3. Find the interquartile range.

   Interactive popup. Assistance may be required.

   Need a hint?

   First, find the median of the first and third quartiles, and then subtract the median of each quartile.
   Interactive popup. Assistance may be required.

   Check Your Answer

   The median values in the first and third quartiles are 13 and 18 respectively, so the interquartile range (IQR) is 5.